Hàm số y = x 4 - 2 m x 2 + m có ba điểm cực trị và đường tròn đi qua ba điểm cực trị này có bán kính bằng 1 thì giá trị của m là:
A. m = 1; m = - 1 ± 5 2
B. m = -1; m = - 1 + 5 2
C. m = 1; m = - 1 + 5 2
D. m = 1; m = - 1 - 5 2
Những câu hỏi liên quan
Cho hàm số \(y=x^4-2mx^2+1\), với m là tham số thực. Tìm m để đồ thị hàm số trên có 3 cực trị và đường tròn đi qua 3 điểm này có bán kính bằng 1
Gọi \(H=BC\cap Oy\) thì AH là đường cao tam giác ABC
Ta có \(H\left(0;c-\frac{b^2}{4a}\right)\Rightarrow AH=\frac{b^2}{4\left|a\right|}\)
\(\sin\widehat{ACH}=\frac{AH}{AC}=\frac{AH}{AB}\Rightarrow R=\frac{AB}{2\sin\widehat{ACH}}=\frac{AB^2}{2AH}=\frac{b^3-8a}{8\left|a\right|b}\)
Từ yêu cầu bài toán \(\Leftrightarrow\begin{cases}ab< 0\\R=1\end{cases}\) \(\Leftrightarrow\begin{cases}m>0\\m^3-2m+1=0\end{cases}\)
\(\Leftrightarrow m=1\) hoặc \(m=\frac{-1+\sqrt{5}}{2}\)
Đúng 0
Bình luận (0)
Cho hàm số
y
1
4
x
4
-
(
m
+
1
2
)
x
2
có đồ thị (C). Có bao nhiêu giá trị thực của tham số m để (C) có ba điểm cực trị và đường tròn qua ba điểm cực trị này đồng thời đi qua điểm A(
-
3
2
;). A. 3. B. 1. C. 4. D. 2.
Đọc tiếp
Cho hàm số y = 1 4 x 4 - ( m + 1 2 ) x 2 có đồ thị (C). Có bao nhiêu giá trị thực của tham số m để (C) có ba điểm cực trị và đường tròn qua ba điểm cực trị này đồng thời đi qua điểm A( - 3 2 ;).
A. 3.
B. 1.
C. 4.
D. 2.
Cho hàm số
y
-
x
3
-
3
x
2
+
4
(
1
)
và đường tròn
(
C
)
:
x
-
m
2
+
y
-
m
-...
Đọc tiếp
Cho hàm số y = - x 3 - 3 x 2 + 4 ( 1 ) và đường tròn ( C ) : x - m 2 + y - m - 2 2 = 20 .Biết rằng có hai giá trị m 1 , m 2 , của tham số m để đường thẳng đi qua hai điểm cực trị của đồ thị hàm số (1) tiếp xúc với đường tròn (C). Tính tổng m 1 + m 2
A. m 1 + m 2 = - 4
B. m 1 + m 2 = 10
C. m 1 + m 2 = 8
D. m 1 + m 2 = 0
Chọn A
Ta có 
và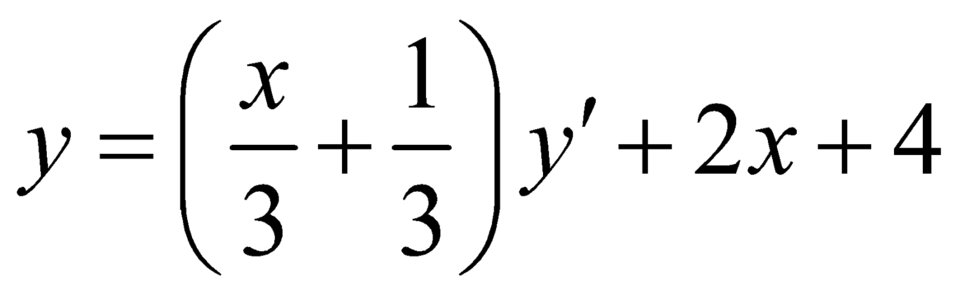 
,
Duy ra phương trình đường thẳng đi qua hai điểm cực trị của đồ thị hàm số là 
, 
.
Đường tròn 
có tâm 
và bán kính 
.
Đường thẳng 
tiếp xúc với đường tròn 
khi và chỉ khi 
.
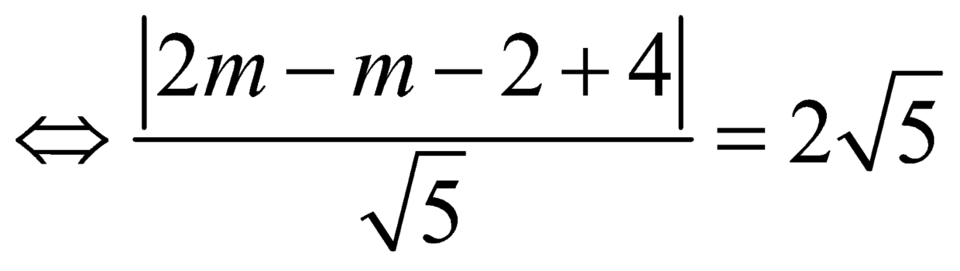
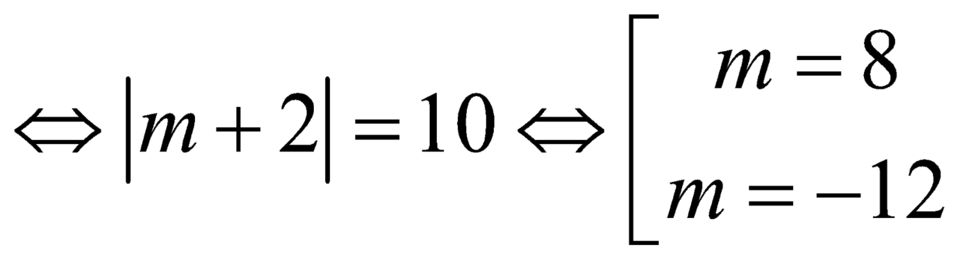Vậy 
.
Đúng 0
Bình luận (0)
Cho hàm số y = x^4 + 2(m + 1)x^2 + 1
a) Khảo sát và vẽ đồ thị khi m = 1
b) Tìm m để đồ thị hàm số có 3 điểm cực trị. Tìm phương trình đường cong đi qua các điểm cực trị đó
b.
y = x^4 + 2(m + 1)x^2 + 1
y' = 4x^3 + 4(m + 1)x
y'= 0=> x=0 và x^2 + (m + 1)= 0 (*)
để đồ thị hàm số có 3 điểm cực trị thì (*) có 2 nghiệm phân biệt
=> m+1<0
<=> m< -1
ta có:
y= [4x^3 + 4(m + 1)x]*x/4+ (m+1)x^2+ 1
y= y'*x/4+ (m+1)x^2+ 1
đường cong đi qua các điểm cực trị thỏa mãn y'= 0
=> pt phương trình đường cong đi qua các điểm cực trị đó là:
y= (m+1)x^2+ 1
Vậy để đồ thị hàm số có 3 điểm cực trị thì m< -1
và pt phương trình đường cong đi qua các điểm cực trị đó là:
y= (m+1)x^2+ 1
Đúng 0
Bình luận (0)
b.
y = x^4 + 2(m + 1)x^2 + 1
y' = 4x^3 + 4(m + 1)x
y'= 0=> x=0 và x^2 + (m + 1)= 0 (*)
để đồ thị hàm số có 3 điểm cực trị thì (*) có 2 nghiệm phân biệt
=> m+1<0
<=> m< -1
ta có:
y= [4x^3 + 4(m + 1)x]*x/4+ (m+1)x^2+ 1
y= y'*x/4+ (m+1)x^2+ 1
đường cong đi qua các điểm cực trị thỏa mãn y'= 0
=> pt phương trình đường cong đi qua các điểm cực trị đó là:
y= (m+1)x^2+ 1
Vậy để đồ thị hàm số có 3 điểm cực trị thì m< -1
và pt phương trình đường cong đi qua các điểm cực trị đó là:
y= (m+1)x^2+ 1
Đúng 0
Bình luận (0)
Cho hàm số
y
x
3
-
3
m
x
2
+
2
(
m
2
-
1
)
x
-
m
3
-
m
(m là tham số). Gọi A, B là hai điểm cực trị của đồ thị hàm số và I(2;-2). Tổng tất cả các giá trị của m để ba điểm I, A, B tạo thành tam giác nội tiếp đường tròn có bán kính bằ...
Đọc tiếp
Cho hàm số y = x 3 - 3 m x 2 + 2 ( m 2 - 1 ) x - m 3 - m (m là tham số). Gọi A, B là hai điểm cực trị của đồ thị hàm số và I(2;-2). Tổng tất cả các giá trị của m để ba điểm I, A, B tạo thành tam giác nội tiếp đường tròn có bán kính bằng 5 là
A. 20 17
B. - 2 17
C. 4 17
D. 14 17
Cho hàm số
y
-
x
4
+
(
2
m
+
1
2
)
x
2
có đồ thị (C). Tổng tất cả các giá trị thực của tham số m để (C) có ba điểm cực trị và đường tròn qua ba điểm cực trị này cũng đi qua điểm A(
9
8
;9/8) là A.
-
2
+...
Đọc tiếp
Cho hàm số y = - x 4 + ( 2 m + 1 2 ) x 2 có đồ thị (C). Tổng tất cả các giá trị thực của tham số m để (C) có ba điểm cực trị và đường tròn qua ba điểm cực trị này cũng đi qua điểm A( 9 8 ;9/8) là
A. - 2 + 33 4
B. - 1 + 2 33 4
C. 3 4
D. - 1 + 33 4
Cho hàm số
y
x
4
-
2
m
x
2
+
1
1
. Tổng lập phương các giá trị của tham số m để đồ thị hàm số (1) có ba điểm cực trị và đường tròn đi qua 3 điểm này có bán kính
R
1
bằng A.
5
-
5...
Đọc tiếp
Cho hàm số y = x 4 - 2 m x 2 + 1 1 . Tổng lập phương các giá trị của tham số m để đồ thị hàm số (1) có ba điểm cực trị và đường tròn đi qua 3 điểm này có bán kính R = 1 bằng
A. 5 - 5 2
B. 1 + 5 2
C. 2 + 5
D. - 1 + 5
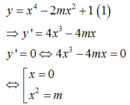
Để đồ thị hàm số có 3 điểm cực trị thì m > 0 .
Khi đó, tọa độ ba điểm cực trị là:
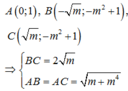
Độ dài đường cao AH của ∆ A B C là:
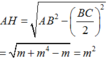
Diện tích ∆ A B C là:
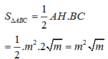
Và
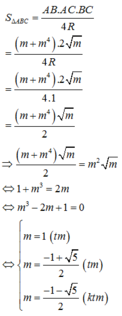
Tổng lập phương các giá trị của tham số m là:
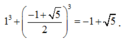
Chọn: D
Đúng 0
Bình luận (0)
Tìm tất cả các giá trị \(m\) để đồ thị hàm số \(y=x^4-2mx^2+m-1\) có các điểm cực trị tạo thành tam giác có bán kính đường tròn ngoại tiếp bằng 1.
Y=x^4-2(m+1)x^2+m^2 a)tìm m để hàm số có 3 cực trị tạo thành 1 tam giác nhận gốc toạ độ o là trọng tâm b)tìm m để hàm số có 3 cực trị tạo thành 3 đỉnh tam giác đều c)tìm m để hàm số có 3 cực trị tạo thành tam giác có bán kính đường tròn ngoại tiếp bằng 1 d) tìm m để hàm số có 3 cực trị và khoảng cách giữa 2 điểm cực tiểu là 5