Cho hình hộp A B C D . A ' B ' C ' D ' có B A D ^ = B A A ' ^ = D A A ' ^ = 60 0 , A B = A D = A A ' = a . Đường thẳng AC’ cắt các mặt phẳng ( A ' B D ) và ( C B ' D ' ) lần lượt tại M và N. Độ dài đoạn thẳng MN bằng
Những câu hỏi liên quan
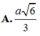
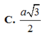
Cho hình hộp chữ nhật ABCD. A'B'C'D' có AB bằng a. Diện tích của ABCD va ABC'D' lần có AA'=a√2, AB=a; A'C=3a. Tính thể tích hình hộp chữ nhật
Cho hình hộp chữ nhật A,B,C,D,A’,B’,C’,D’
a) AB=5cm ,AD=7cm ,AA’=3cm .Hãy tính diện tích xung quanh,thể tích của hình hộp chữ nhật
Diện tích xung quanh:
2 x 3 x (5+7)= 72(cm2)
Thể tích của HHCN:
3 x 5 x 7 = 105(cm3)
Đúng 0
Bình luận (0)
Cho hình hộp chữ nhật A,B,C,D,A’,B’,C’,D’ a) AB=5cm ,AD=7cm ,AA’=3cm .Hãy tính diện tích xung quanh,thể tích của hình hộp chữ nhật
Sxq=(5+7)*2*3=6*12=72cm2
V=5*7*3=105cm3
Đúng 0
Bình luận (0)
11 tháng 9 2021 lúc 17:05
Câu 2. Cho hình hộp thoi ABCD.ABCD có tất cả các cạnh bằng a và các góc ABC BBA BBC 60o. Chứng minh tứ giác ABCD là hình vuông. Câu 3. Cho hình hộp ABCD.ABCD có độ dài tất cả các cạnh bằng a và các góc BAD, DAA , AAB đều bằng 60o . Gọi M, N lần lượt là trung điểm của AA , CD. Gọi α là góc tạo bởi hai đường thẳng MN và BC. Tính cos αCâu 4. Cho hình chóp S.ABCD, có đáy ABCD là hình vuông tâm O, cạnh bằng a; SA vuông góc với đáy và SA a√3. Khi đó, cosin góc giữa SB và AC bằng
Đọc tiếp
Câu 2. Cho hình hộp thoi ABCD.A'B'C'D' có tất cả các cạnh bằng a và các góc ABC = B'BA = B'BC = 60o. Chứng minh tứ giác A'B'CD là hình vuông.
Câu 3. Cho hình hộp ABCD.A'B'C'D' có độ dài tất cả các cạnh bằng a và các góc BAD, DAA' , A'AB đều bằng 60o . Gọi M, N lần lượt là trung điểm của AA' , CD. Gọi α là góc tạo bởi hai đường thẳng MN và B'C. Tính cos α
Câu 4. Cho hình chóp S.ABCD, có đáy ABCD là hình vuông tâm O, cạnh bằng a; SA vuông góc với đáy và SA = a√3. Khi đó, cosin góc giữa SB và AC bằng
Câu 1: Hình hộp chữ nhật có:A. 6 cạnh B. 10 cạnhC. 8 cạnh D. 12 cạnhCâu 2: Hình hộp chữ nhật có:A. 4 mặt B.5 mặtC. 6 mặt D. 8 mặtCâu 3: Tính diện tích mặt đáy của hình hộp chữ nhật hình có chiều dài a, chiều rộng b , chiều cao h ( cùng đơn vị đo) được tính theo công thức:A. S a+bx2 C. S a x bB. (a+b)x2 D. a: bCâu 4: Diện tích xung quanh của hình hộp chữ nhật là diện tích của:A. 2 mặt đáyB. 4 mặt xung quanhC. 2 mặt xung quanhD. 6 mặtCâu 5: Chu vi mặt đáy của hình hộp chữ nhật có chiều dài 1,5dm...
Đọc tiếp
Câu 1: Hình hộp chữ nhật có:
A. 6 cạnh B. 10 cạnh
C. 8 cạnh D. 12 cạnh
Câu 2: Hình hộp chữ nhật có:
A. 4 mặt B.5 mặt
C. 6 mặt D. 8 mặt
Câu 3: Tính diện tích mặt đáy của hình hộp chữ nhật hình có chiều dài a, chiều rộng b , chiều cao h ( cùng đơn vị đo) được tính theo công thức:
A. S = a+bx2 C. S = a x b
B. (a+b)x2 D. a: b
Câu 4: Diện tích xung quanh của hình hộp chữ nhật là diện tích của:
A. 2 mặt đáy
B. 4 mặt xung quanh
C. 2 mặt xung quanh
D. 6 mặt
Câu 5: Chu vi mặt đáy của hình hộp chữ nhật có chiều dài 1,5dm, chiều rộng 1,2dm chiều cao 1dm là:
A. 5,4dm B. 2,5dm
C. 2,7dm D. 5 dm
Câu 1: Hình hộp chữ nhật có:
A. 6 cạnh B. 10 cạnh
C. 8 cạnh D. 12 cạnh
Câu 2: Hình hộp chữ nhật có:
A. 4 mặt B.5 mặt
C. 6 mặt D. 8 mặt
Câu 3: Tính diện tích mặt đáy của hình hộp chữ nhật hình có chiều dài a, chiều rộng b , chiều cao h ( cùng đơn vị đo) được tính theo công thức:
A. S = a+bx2 C. S = a x b
B. (a+b)x2 D. a: b
Câu 4: Diện tích xung quanh của hình hộp chữ nhật là diện tích của:
A. 2 mặt đáy
B. 4 mặt xung quanh
C. 2 mặt xung quanh
D. 6 mặt
Câu 5: Chu vi mặt đáy của hình hộp chữ nhật có chiều dài 1,5dm, chiều rộng 1,2dm chiều cao 1dm là:
A. 5,4dm B. 2,5dm
C. 2,7dm D. 5 dm
Lời giải chi tiết: Chu vi mặt đáy là:
(1,5+1,2)×2=5,4(dm)
Đáp số: 5,4dm
Cho hình hộp chữ nhật ABCD.A′B′C′D′ có đáy là hình vuông cạnh a và cạnh bên bằng 3a. Diện tích xung quanh Sxq của hình nón có đỉnh là tâm O của hình vuông A′B′C′D′ và có đáy là hình tròn nội tiếp hình vuông ABCD là A.
S
xq
13
πa
2
4
B.
S
xq...
Đọc tiếp
Cho hình hộp chữ nhật ABCD.A′B′C′D′ có đáy là hình vuông cạnh a và cạnh bên bằng 3a. Diện tích xung quanh Sxq của hình nón có đỉnh là tâm O của hình vuông A′B′C′D′ và có đáy là hình tròn nội tiếp hình vuông ABCD là
A. S xq = 13 πa 2 4
B. S xq = 37 πa 2 12
C. S xq = 13 πa 2 12
D. S xq = 37 πa 2 4
1.Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi A',B' lần lượt là trung điểm của SA,SB . Đường thẳng A' B' song song với mặt phẳng nào dưới đây?
A. (SAB).
B. ( ABCD) .
C. (SAD).
D. (SBC).
2.Cho hình hộp ABCD.A' B' C' D' . Mặt phẳng ( ABA') song song với:
A. ( AA'C') .
B. (CC'D').
C. ( ADD').
D. (BB'A').
cho hình hộp chữ nhật ABCD . A'B'C'D' ; có AB = 10cm ; BC = 20cm ; AA' = 15cm
a) tính thể tích hình hộp chữ nhật
b) tính độ dài đường chéo AC' của hình hộp chữ nhật
10 tháng 5 2018 lúc 20:51
a) Diện tích đáy hình hộp chữ nhật:
Thể tích hình hộp chữ nhật:
b) tam giác A'B'C' vuông tại B. Áp dụng định lý PITAGO ta có:
Đúng 0
Bình luận (0)
Hình hộp ABCD.A′B′C′D′ có
A
0
;
0
;
1
,
B
−
1
;
1
;
0
,
D
−
2
;
−
1
;
0
,...
Đọc tiếp
Hình hộp ABCD.A′B′C′D′ có A 0 ; 0 ; 1 , B − 1 ; 1 ; 0 , D − 2 ; − 1 ; 0 , A ' 1 ; 1 ; 0 . Tọa độ đỉnh C′ là
A. 1 ; − 1 ; − 2
B. 0 ; 1 ; − 2
C. − 2 ; 1 ; − 2
D. 2 ; 1 ; − 2
Cho hình hộp chữ nhật ABCD.A′B′C′D′ có
A
B
a
,
A
A
2
a
.
Biết thể tích hình cầu ngoại tiếp tứ diện ABCD′ là
9
π
2
a
3
. Tính thể tích V của hình chữ nhật ABCD.A′B′C′D′. A.
4
a
3
B. ...
Đọc tiếp
Cho hình hộp chữ nhật ABCD.A′B′C′D′ có A B = a , A A ' = 2 a . Biết thể tích hình cầu ngoại tiếp tứ diện ABCD′ là 9 π 2 a 3 . Tính thể tích V của hình chữ nhật ABCD.A′B′C′D′.
A. 4 a 3
B. 4 a 3 3
C. 2 a 3
D. 2 a 3 3
