Cho hàm số y=f(x) liên tục trên R và có đồ thị như hình vẽ dưới. Xét hàm số g ( x ) = f ( 2 x 3 + x - 1 ) + m . Tìm m để m a x 0 ; 1 g x = - 10
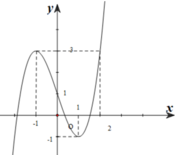
A. m = -13
B. m = 5
C. m = 3
D. m = -1
Cho hàm số y=f(x) có đạo hàm liên tục trên R và có đồ thị hàm y=f '(x) như hình vẽ. xét hàm số g(x)=f(2-x^2). Mệnh đề nào dưới đây sai?
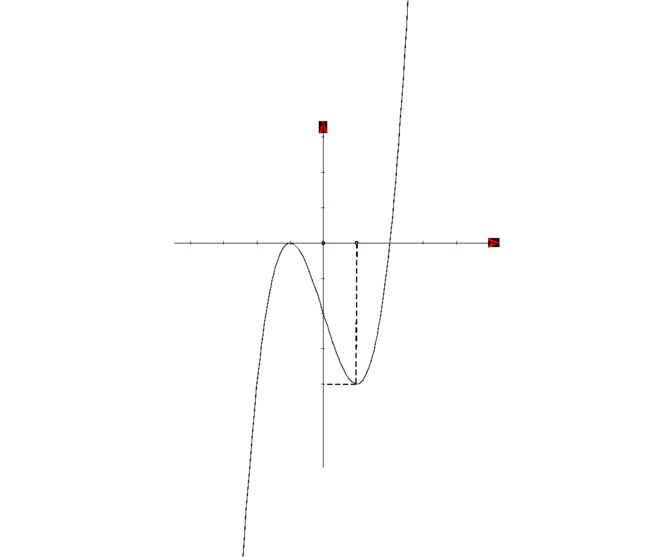
A. Hàm số ![]() đạt cực trị tại
đạt cực trị tại ![]() .
.
B. Hàm số ![]() nghịch biến trên
nghịch biến trên ![]() .
.
C. Hàm số ![]() đồng biến trên
đồng biến trên ![]() .
.
D. Hàm số ![]() đồng biến trên
đồng biến trên ![]() .
.
Cho hàm số y=f(x) có đạo hàm liên tục trên R và có đồ thị hàm y = f'(x) như hình vẽ. xét hàm số g x = f 2 - x 2 . Mệnh đề nào dưới đây sai?
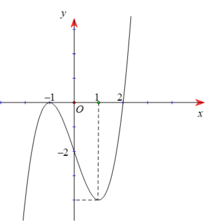
A. Hàm số f(x) đạt cực trị tại x=2.
B. Hàm số f(x) nghịch biến trên - ∞ ; 2 .
C. Hàm số g(x) đồng biến trên 2 ; + ∞ .
D. Hàm số g(x) đồng biến trên (-1;0).
Cho hàm số y=f(x) có đạo hàm trên R. Đường cong hình vẽ bên là đồ thị hàm số y=f '(x) (Hàm số y=f '(x) liên tục trên R. Xét hàm số g ( x ) = f ( x 2 - 2 ) . Mệnh đề nào dưới đây là sai?
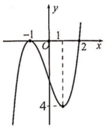
A. Hàm số y=g(x) đồng biến trên khoảng (-2;-1)
B. Hàm số y=g(x) đồng biến trên khoảng 2 ; + ∞
C. Hàm số y=g(x) nghịch biến trên khoảng (-1;0)
D. Hàm số y=g(x) nghịch biến trên khoảng (0;2)
Cho hàm số y = f(x) có đạo hàm trên R. Đường cong trong hình vẽ bên là đồ thị của hàm số y = f’(x), (y = f’(x) liên tục trên R). Xét hàm số g(x) = f(x2 - 2). Mệnh đề nào dưới đây sai?

A. Hàm số g(x) nghịch biến trên (-∞;-3)
B. Hàm số g(x) có 3 điểm cực trị
C. Hàm số g(x) nghịch biến trên (-1;0)
D. Điểm cực đại của hàm số là 0
cho hàm số y=f(x) liên tục trên R và có đồ thị như hình vẽ. Xét hàm số g(x)=f(x^3+2x-1)+4m. Tìm m để ming(x)=5
\(g’\left( x \right) = \left( {3{x^2} + 1} \right)f’\left( {{x^3} + x – 1} \right)\)
Xét \(g’\left( x \right) = 0 \Leftrightarrow f’\left( {{x^3} + x – 1} \right) = 0\)
\( \Leftrightarrow \left[ \begin{array}{l}{x^3} + x – 1 = – 1\\{x^3} + x – 1 = 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}{x^3} + x = 0\\{x^3} + x – 2 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 1\end{array} \right.\).
\(\begin{array}{l}g\left( 0 \right) = f\left( { – 1} \right) + m = 3 + m\\g\left( 1 \right) = f\left( 1 \right) + m = – 1 + m\end{array}\)
\(\begin{array}{l} \Rightarrow \mathop {\max }\limits_{\left[ {0;1} \right]} g\left( x \right) = g\left( 0 \right)\\ \Rightarrow 3 + m = – 10\\ \Leftrightarrow m = – 13\end{array}\)
Cho hàm số y = f(x) có đạo hàm liên tục trên R. Đường cong trong hình vẽ bên là đồ thị của hàm số y = f’(x). Xét hàm số g(x) = f(x2 – 3). Mệnh đề nào dưới đây sai ?
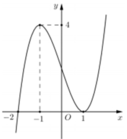
A. Hàm số g(x) đồng biến trên (–1;0)
B. Hàm số g(x) nghịch biến trên (–∞;–1)
C. Hàm số g(x) nghịch biến trên (1;2)
D. Hàm số g(x) đồng biến trên (2;+ ∞)
Đáp án C.
Ta có ![]() ∀
x
∈
R
∀
x
∈
R
Khi đó ![]()
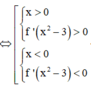
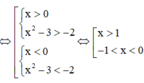
Suy ra hàm số đồng biến trên khoảng (–1;0) và (1;+ ∞)
Cho hàm số y=f(x) xác định và liên tục trên R, có đồ thị hàm số y=f’(x) như hình vẽ bên dưới. Hàm số g(x)=f(x) – 1/2 x2+ x-8 có bao nhiêu điểm cực tiểu?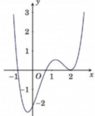
A. 3
B. 2
C. 1.
D. 4
Cho hàm số y= f( x) liên tục và xác định trên R. Biết f( x) có đạo hàm f’(x) và hàm số y= f’(x) có đồ thị như hình vẽ. Xét trên ![]() , khẳng định nào sau đây đúng?
, khẳng định nào sau đây đúng?
A. Hàm số y= f( x) đồng biến trên khoảng ![]() .
.
B. Hàm số y= f( x) nghịch biến trên khoảng ![]() .
.
C. Hàm số y= f(x) nghịch biến trên khoảng - π ; - π 2 và π 2 ; π .
D. Hàm số y= f( x) đồng biến trên khoảng ![]() .
.
Chọn D
Trong khoảng ![]() đồ thị hàm số y= f’(x) nằm phía trên trục hoành nên hàm số y= f( x) đồng biến trên khoảng ( 0; π)
đồ thị hàm số y= f’(x) nằm phía trên trục hoành nên hàm số y= f( x) đồng biến trên khoảng ( 0; π)
Cho hàm số y=f(x) có đạo hàm liên tục trên R và có đồ thị hàm số y=f '(x) như hình vẽ bên dưới. Xét hàm số g(x)=f(x^2-3) và các mệnh đề sau:
I. Hàm số ![]() có 3 điểm cực trị.
có 3 điểm cực trị.
II. Hàm số g(x)đạt cực tiểu tại x=0
III. Hàm số g(x) đạt cực đại tại x=2
IV. Hàm số g(x) đồng biến trên khoảng (-2;0)
V. Hàm số g(x) nghịch biến trên khoảng (-1;1)
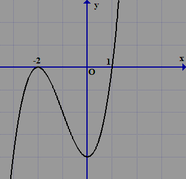
Có bao nhiêu mệnh đề đúng trong các mệnh đề trên?
A.1
B.4
C.3
D.2
Chọn D
Xét hàm số ![]() .
.
Có ![]()
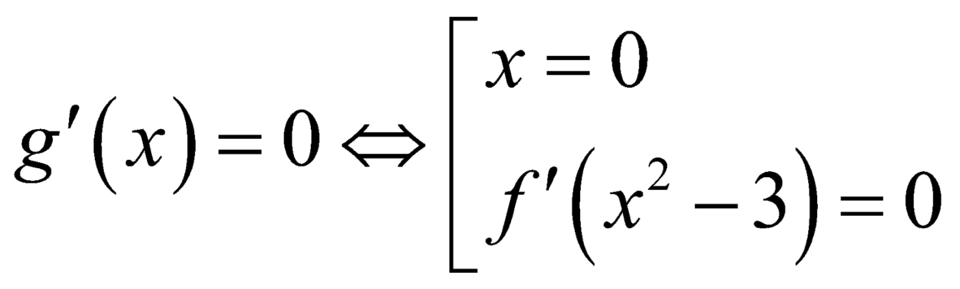
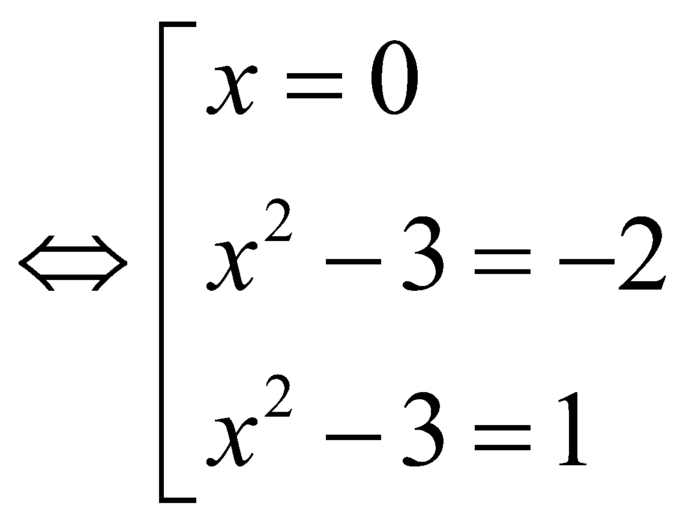
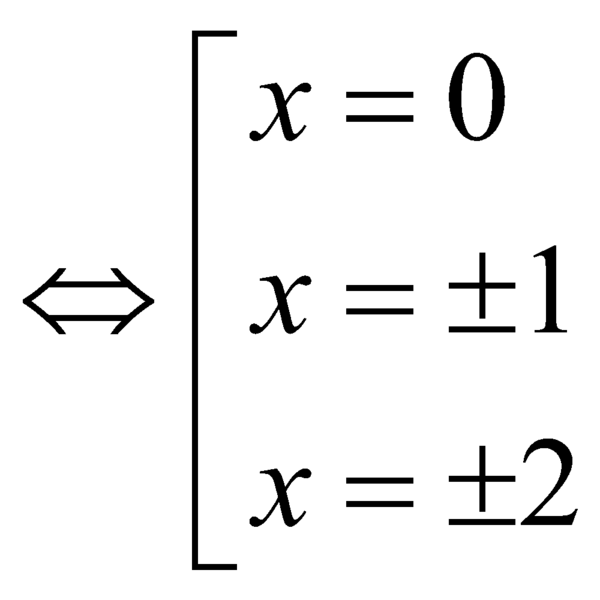 .
.
Ta lại có ![]() thì
thì ![]() . Do đó
. Do đó ![]() thì
thì ![]() .
.
![]() thì
thì ![]() . Do đó
. Do đó ![]() thì
thì ![]() .
.
Từ đó ta có bảng biến thiên của ![]() như sau
như sau
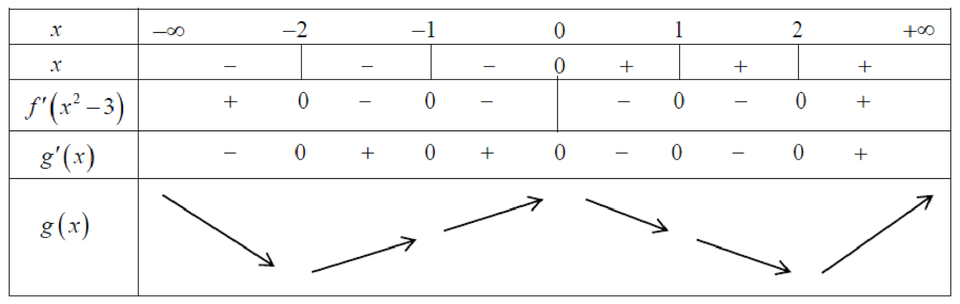
Dựa vào bảng biến thiên, ta có
I. Hàm số ![]() có 3 điểm cực trị . LÀ MỆNH ĐỀ ĐÚNG.
có 3 điểm cực trị . LÀ MỆNH ĐỀ ĐÚNG.
II. Hàm số ![]() đạt cực tiểu tại
đạt cực tiểu tại ![]() LÀ MỆNH ĐỀ SAI.
LÀ MỆNH ĐỀ SAI.
III. Hàm số ![]() đạt cực đại tại
đạt cực đại tại ![]() LÀ MỆNH ĐỀ SAI.
LÀ MỆNH ĐỀ SAI.
IV. Hàm số ![]() đồng biến trên khoảng
đồng biến trên khoảng ![]() LÀ MỆNH ĐỀ ĐÚNG.
LÀ MỆNH ĐỀ ĐÚNG.
V. Hàm số ![]() nghịch biến trên khoảng
nghịch biến trên khoảng ![]() LÀ MỆNH ĐỀ SAI.
LÀ MỆNH ĐỀ SAI.
Vậy có hai mệnh đề đúng.
ở chỗ x<1=> x= -2 thì sao bạn ơi =>(x^2 -3) =1 >0 thì sao f ' (...)>0 được ????