Cho cấp số cộng ( u n ) và gọi S n là tổng n số hạng đầu tiên của nó. Biết S 7 = 77 , S 1 2 = 192 . Tìm số hạng tổng quát u n của cấp số cộng đó
A. u n =5+4n
B. u n =3+2n x
C. u n =2+3n
D. u n =4+5n
Cho cấp số cộng ( u n ) và gọi S n là tổng n số hạng đầu tiên của nó. Biết S 7 = 77 v à S 12 = 192 . Tìm số hạng tổng quát u n của cấp số cộng đó
A. u n = 5 + 4 n .
B. u n = 3 + 2 n .
C. u n = 2 + 3 n .
D. u n = 4 + 5 n .
Cho cấp số cộng u n và gọi S n là tổng n số hạng đầu tiên của nó. Biết S 7 = 77 và S 12 = 192 . Tìm số hạng tổng quát u n của cấp số cộng đó.
A. u n = 5 + 4 n
B. u n = 3 + 2 n
C. u n = 2 + 3 n
D. u n = 4 + 5 n
Chọn đáp án B
Giả sử cấp số cộng có số hạng đầu là u 1 và công sai d.
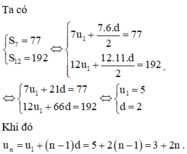
Cho cấp số cộng ( u n ) và gọi S n là tổng n số hạng đầu tiên của nó. Biết S 7 = 77 và S 12 = 192 . Tìm số hạng tổng quát un của cấp số cộng đó.
A. u n = 5 + 4 n
B. u n = 3 + 2 n
C. u n = 2 + 3 n
D. u n = 4 + 5 n
Cho cấp số cộng u n có tổng của n số hạng đầu tiên được tính bởi công thức S n = 4 n – n ^ 2. Gọi M là tổng của số hạng đầu tiên và công sai của cấp số cộng. Khi đó:
A. M = -1
B. M = 1
C. M = 4
D. M = 7
Chọn B.
- Ta có: u 1 = S 1 = 3 .
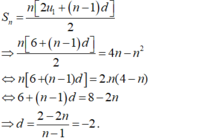
- Vậy M = u 1 + d = 3 - 2 = 1 .
Cho một cấp số nhân có n số hạng. Số hạng đầu tiên là 1, công bội là q và tổng là S. Trong đó q và S đều khác 0. Tổng các số hạng của cấp số nhân mới được thành bằng cách thay đổi mỗi số hạng của cấp số nhân ban đầu bằng nghịch đảo của nó là:
A. 1 S .
B. 1 q n . S .
C. S q n − 1 .
D. q n S .
Đáp án C
Em có: S = 1. q n − 1 q − 1 = q n − 1 q − 1 .
Vì cấp số nhân mới tạo thành bằng cách thay đổi mỗi số hạng của cấp số nhân ban đầu thành nghịch đảo của nó nên cấp số nhân mới sẽ có công bội là 1 q .
Gọi S' là tổng mới của cấp số nhân mới.
Em có: S ' = 1 q n − 1 1 q − 1 = 1 − q n q n . 1 − q q = 1 − q n 1 − q . 1 q n − 1 = S q n − 1 .
Vậy tổng của cấp số nhân mới là: S q n − 1 .
Cho cấp số cộng có tổng của n số hạng đầu tiên được tính bởi công thức S n = 4 n − n 2 . Gọi M là tổng của số hạng đầu tiên và công sai của cấp số cộng đó. Khi đó :
A. M=7
B. M=4
C. M= -1
D. M=1
Đáp án D
S = 1 u = 1 3 S = 2 2 u + 1 d = 4 ⇒ u = 1 3 d = − 2 ⇒ M = 1
Cho cấp số cộng có tổng của n số hạng đầu tiên được tính bởi công thức S n = 4 n − n 2 . Gọi M là tổng của số hạng đầu tiên và công sai của cấp số cộng đó. Khi đó :
A. M = 7
B. M = 4
C. M = -1
D. M = 1
Đáp án D
Ta có: S = 1 u = 1 3 S = 2 2 u + 1 d = 4 ⇒ u = 1 3 d = − 2 ⇒ M = 1
Cho cấp số cộng có tổng của n số hạng đầu tiên được tính bởi công thức Sn = 4n – n2. Gọi M là tổng của số hạng đầu tiên và công sai của cấp số cộng đó. Khi đó :
A. M = 7
B. M = 4
C. M = 2
D. M = 1
Theo đề, ta có: \(S_n=3003\)
=>\(n\cdot\dfrac{\left[2u1+\left(n-1\right)\cdot d\right]}{2}=3003\)
=>\(\dfrac{n\left[2+\left(n-1\right)\right]}{2}=3003\)
=>n(n+1)=6006
=>n^2+n-6006=0
=>(n-77)(n+78)=0
=>n=77(nhận) hoặc n=-78(loại)
Vậy: n=77