Cho các số thực a, b khác 0. Xét hàm số f x = a x + 1 3 + b x e x với ∀ x ≠ − 1. Biết f ' x = f 0 = − 22 v à ∫ 0 1 f x d x = 5 . Tính a + b .
A. 19
B. 7
C. 8
D. 10
Những câu hỏi liên quan
Cho các số thực a, b khác 0. Xét hàm số
f
(
x
)
a
(
x
+
1
)
3
+
b
x
e
x
với mọi x khác -1. Biết f(0)-22 và...
Đọc tiếp
Cho các số thực a, b khác 0. Xét hàm số f ( x ) = a ( x + 1 ) 3 + b x e x với mọi x khác -1. Biết f'(0)=-22 và ∫ 0 1 f ( x ) d x = 5 . Tính a 2 + b 2 .
A. 42
B. 72
C. 68
D. 10
Cho các số thực a, b khác 0. Xét hàm số
f
(
x
)
a
(
x
+
1
)
3
+
b
x
e
x
với mọi x khác -1. Biết f(0)-22 và
∫
0
1
f
(
x
)
d
x...
Đọc tiếp
Cho các số thực a, b khác 0. Xét hàm số f ( x ) = a ( x + 1 ) 3 + b x e x với mọi x khác -1. Biết f'(0)=-22 và ∫ 0 1 f ( x ) d x = 5 . Tính a 2 + b 2
A. 42
B. 72
C. 68
D. 10
Cho các số thực a, b khác 0. Xét hàm số
f
x
a
x
+
1
3
+
b
x
e
x
với
∀
x
≠
−
1.
Biết
f
0
−
22
và
∫...
Đọc tiếp
Cho các số thực a, b khác 0. Xét hàm số f x = a x + 1 3 + b x e x với ∀ x ≠ − 1. Biết f ' 0 = − 22 và ∫ 0 1 f x d x = 5. Tính a + b
A. 19
B. 7
C. 8
D. 10
Đáp án A
Ta có:
∫ 0 1 f x d x = ∫ 0 1 a x + 1 3 d x + ∫ 0 1 b x e x d x = − a 2 1 x + 1 2 0 1 + ∫ 0 1 b x e x d x = 3 a 8 + ∫ 0 1 b x e x d x
Đặt:
u = x d v = e x d x ⇒ d u = d x v = e x ⇒ ∫ 0 1 b x e x d x = b x e x 0 1 − ∫ 0 1 b e x d x = b x e x 0 1 − b e x 0 1 = b
Suy ra ∫ 0 1 f x d x = 3 a 8 + b = 5 1
Mặt khác f ' x = − 3 a x + 1 4 + b e x + b x e x ⇒ f ' 0 = − 3 a + b = − 22 2
Từ 1 , 2 suy ra a = 8 ; b = 2 ⇒ a + b = 10
Đúng 0
Bình luận (0)
Cho các số thực a, b khác không. Xét hàm số
f
x
a
x
+
1
3
+
b
x
e
x
với mọi x khác –1. Biết f’(0) –22 và
∫
0
1
f
x
d
x
5
. Tính a...
Đọc tiếp
Cho các số thực a, b khác không. Xét hàm số f x = a x + 1 3 + b x e x với mọi x khác –1. Biết f’(0) = –22 và ∫ 0 1 f x d x = 5 . Tính a + b?
A. 19.
B. 7.
C. 8.
D. 10.
Chọn D
Ta có
f ' x = - 3 a x + 1 4 + b e x + b x e x
nên f’(0) = x – 3a + b = –22 (1).
Xét
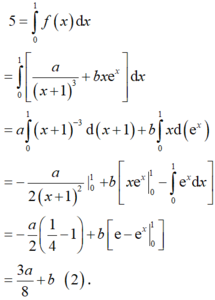
Từ (1) và (2) ta có
Đúng 0
Bình luận (0)
Xét các số thực xba0. Cho hàm số yf(x) có đạo hàm liên tục trên R và có bảng xét dấu của đạo hàm như hình vẽ. Đặt
g
x
f
x
3
Số điểm cực trị của hàm số yg(x) là A. 3 B. 7 C. 4 D. 5
Đọc tiếp
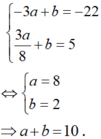
Xét các số thực x>b>a>0. Cho hàm số y=f(x) có đạo hàm liên tục trên R và có bảng xét dấu của đạo hàm như hình vẽ. Đặt g x = f x 3 Số điểm cực trị của hàm số y=g(x) là
A. 3
B. 7
C. 4
D. 5
Cho hàm số
y
f
(
x
)
có đạo hàm trên khoảng
a
;
b
. Xét các mệnh đề sau: I. Nếu hàm số
y
f
(
x
)
đồng biến trên khoảng
a
;
b
thì
f...
Đọc tiếp
Cho hàm số y = f ( x ) có đạo hàm trên khoảng a ; b . Xét các mệnh đề sau:
I. Nếu hàm số y = f ( x ) đồng biến trên khoảng a ; b thì f ' x > 0 , ∀ x ∈ a ; b .
II. Nếu f ' x < 0 , ∀ x ∈ a ; b thì hàm số y = f ( x ) nghịch biến trên khoảng a ; b .
III. Nếu hàm số y = f ( x ) liên tục trên a ; b và f ' x > 0 , ∀ x ∈ a ; b thì hàm số y = f ( x ) đồng biến trên đoạn a ; b .
Số mệnh đề đúng là:
A. 3
B. 0
C. 2
D. 1
Đáp án là C
I.Sai ví dụ hàm số y = x 3 đồng biến trên
(−¥; +¥) nhưng y' ³ 0, "x Î (−¥; +¥)
II.Đúng
III.Đúng
Đúng 0
Bình luận (0)
Cho a,b,c,d là các số thực khác 0 và hàm số yf(x) asincx + bcosdx. Khẳng định nào sau đây là đúng? A. yf(x) asincx + bcosdx là hàm số tuần hoàn khi và chỉ khi
c
d
là số hữu tỉ. B. yf(x) asincx + bcosdx là hàm số tuần hoàn khi và chỉ khi
a
d
là số hữu tỉ. C. yf(x) asincx + bcosdx là hàm số tuần hoàn khi và chỉ khi
c
b...
Đọc tiếp
Cho a,b,c,d là các số thực khác 0 và hàm số
y=f(x)= asincx + bcosdx. Khẳng định nào sau đây là đúng?
A. y=f(x)= asincx + bcosdx là hàm số tuần hoàn khi và chỉ khi c d là số hữu tỉ.
B. y=f(x)= asincx + bcosdx là hàm số tuần hoàn khi và chỉ khi a d là số hữu tỉ.
C. y=f(x)= asincx + bcosdx là hàm số tuần hoàn khi và chỉ khi c b là số hữu tỉ.
D. y=f(x)= asincx + bcosdx là hàm số tuần hoàn khi và chỉ khi a x là số hữu tỉ.
Chọn A
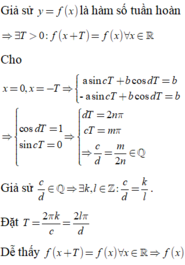
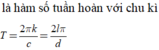
· Bổ trợ kiến thức: Thường thì ở những bài toán như trên các em có thể suy luận được ngay c d mới có sự liên quan và quyết định đến việc hàm số y = f(x)có tuần hoàn hay không.
Tuy nhiên chỉ cần nhận ra được chiều thuận “y= f(x)=asincx+bcosdx là hàm số tuần hoàn => c d là số hữu tỉ” là các em đã thấy ngay được phương án đúng rồi, để chứng minh chiều ngược lại thì đó là điều không dễ dàng.
Các em ghi nhớ luôn nhé – để áp dụng vào các bài tập khác: “Cho a,b,c,d là các số thực khác 0 và hàm số y= f(x)=asincx+bcosdx, khi đó y= f(x)=asincx+bcosdxlà hàm số tuần hoàn khi và chỉ khi c d là số hữu tỉ”
Đúng 0
Bình luận (0)
Cho hàm số
y
f
x
xác định, có đạo hàm trên đoạn
a
;
b
(với
a
b
). Xét các mệnh đề sau: i) Nếu
f
x...
Đọc tiếp
Cho hàm số y = f x xác định, có đạo hàm trên đoạn a ; b (với a < b ). Xét các mệnh đề sau:
i) Nếu f ' x > 0 , ∀ x ∈ a ; b thì hàm số y = f ( x ) đồng biến trên khoảng a ; b .
ii) Nếu phương trình f ' ( x ) = 0 có nghiệm x 0 thì f ' ( x ) đổi dấu từ dương sang âm khi qua x 0 .
iii) Nếu f ' x ≤ 0 , ∀ x ∈ a ; b thì hàm số y = f ( x ) nghịch biến trên khoảng a ; b .
Số mệnh đề đúng trong các mệnh đề trên là:
A. 2
B. 3
C. 0
D. 1
Chọn D
i) Đúng.
ii) Sai, ví dụ: Xét hàm số
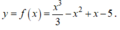
Ta có f ' x = x 2 - 2 x + 1 .
Cho f ' ( x ) ⇔ x = 1 .
Khi đó phương trình f ' ( x ) = 0 có nghiệm x 0 = 1 nhưng đây là nghiệm kép nên không đổi dấu khi qua x 0 .
iii) Sai, vì: Thiếu điều kiện f ' ( x ) = 0 chỉ tại một số hữu hạn điểm.
Vậy có 1 mệnh đề đúng.
Đúng 0
Bình luận (0)
cho hàm số y+ f(x) + (m-1)*x (m khác 1.
a. xét công thức đã cho biết đồ thị hàm số đó đi qua điểm A(1;3)
b. tính f(-1); f(-1/2)
c. tìm x để f(x)=-5; f(x)=-4
d. vẽ đồ thị hàm số đã cho
e. trong các điểm B(-2:4) D(-1;-3); e(1/3;1) điểm nào thuộc đò thị đã cho