Cho M, N là 2 điểm trong mặt phẳng phức biểu diễn số phức z, w khác 0 thỏa mãn z 2 + w 2 = z w . Hỏi tam giác OMN là tam giác gì?
A. Đều
B. Vuông
C. Cân
D. Thường
Cho M,N là 2 điểm trong mặt phẳng phức biểu diễn số phức z, w khác 0 thỏa mãn z 2 + w 2 = z w . Hỏi tam giác OMN là tam giác gì?
A. Đều
B. Vuông
C. Cân
D. Thường
Cho w là số phức thay đổi thỏa mãn w = 2 .
Trong mặt phẳng phức, các điểm biểu diễn số phức z=3w+1-2i chạy trên đường nào?
A. Đường tròn tâm I(1;-2), bán kính R=6
B. Đường tròn tâm I(-1;2), bán kính R=2
C. Đường tròn tâm I(1;-2), bán kính R=2
D. Đường tròn tâm I(-1;2), bán kính R=6
Cho w là số phức thay đổi thỏa mãn w = 2 . Trong mặt phẳng phức, các điểm biểu diễn số phức z = 3 w + 1 − 2 i chạy trên đường nào?
A. Đường tròn tâm I 1 ; − 2 , bán kính R = 6 .
B. Đường tròn tâm I − 1 ; 2 , bán kính R = 2 .
C. Đường tròn tâm I 1 ; − 2 , bán kính R = 2 .
D. Đường tròn tâm I − 1 ; 2 , bán kính R = 6 .
Cho w là số phức thay đổi thỏa mãn w = 2 . Trong mặt phẳng phức, các điểm biểu diễn số phức z = 3 w + 1 - 2 i chạy trên đường nào?
A. Đường tròn tâm I(1;-2), bán kính R = 6.
B. Đường tròn tâm I(-1;2), bán kính R = 2.
C. Đường tròn tâm I (1;-2), bán kính R = 2.
D. Đường tròn tâm I(-1;2), bán kính R = 6.
Cho số phức z thỏa mãn z - 3 + 4 i = 2 và w = 2z + 1 – i. Trong mặt phẳng phức, tập hợp điểm biểu diễn số phức w là đường tròn tâm I, bán kính R . Khi đó:
A. I (-7;9), R = 16
B. I (-7;9), R = 4
C. I (7;-9), R = 16
D. I (7;-9), R = 4.
Cho số phức z thay đổi hoàn toàn thỏa mãn: |z-i| = |z-1+2i|. Tập hợp các điểm trên mặt phẳng tọa độ biểu diễn số phức w thỏa mãn: w = (2-i)z+1 là một đường thẳng. Viết phương trình đường thẳng đó.
A. -x + 7y + 9 = 0
B. x + 7y - 9 = 0
C. x + 7y + 9 = 0
D. x - 7y + 9 = 0
Đáp án C
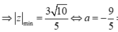
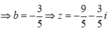
Đặt ![]()
Đặt ![]() Số phức w được biểu diễn bởi điểm M(x';y')
Số phức w được biểu diễn bởi điểm M(x';y')
Em có:

Em có: ![]()
![]()
Mà x = 3y + 2 nên w = ![]()
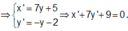
Vậy số phức w được biểu diễn bởi đoạn thẳng: x + 7y + 9 = 0
Xét các số phức z thỏa mãn điều kiện z - 1 + i = 2 Trong mặt phẳng tọa độ Oxy, tập hợp các điểm biểu diễn các số phức w = z + 2 -i là
A. đường tròn tâm I(-3;2), bán kính R = 2.
B. đường tròn tâm I(3;-2), bán kính R = 2.
C. đường tròn tâm I(1;0), bán kính R =2.
D. đường tròn tâm I(1;-1), bán kính R = 2.
Cho số phức z thay đổi hoàn toàn thỏa mãn: z − i = z − 1 + 2 i . Tập hợp các điểm trên mặt phẳng tọa độ biểu diễn số phức w thỏa mãn: w = 2 − i z + 1 là một đường thẳng. Viết phương trình đường thẳng đó.
A. − x + 7 y + 9 = 0.
B. x + 7 y − 9 = 0.
C. x + 7 y + 9 = 0.
D. x − 7 y + 9 = 0.
Đáp án C
Đặt z = x + yi , x ; y ∈ ℝ .
Đặt w = x ' + y ' i , x ' , y ' ∈ ℝ . Số phức w được biểu diễn bởi điểm M x ' ; y ' .
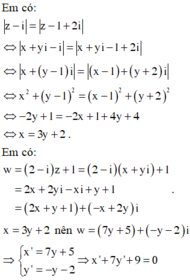
Vậy số phức w được biểu diễn bởi đoạn thẳng: x + 7 y + 9 = 0. .
Cho số phức z thỏa mãn điều kiện z - 2 + 3 i ≤ 3 . Trong mặt phẳng Oxy, tập hợp điểm biểu diễn số phức w = 2 z + 1 - i là hình tròn có diện tích.
![]()
![]()
![]()
![]()