Tìm tất cả các giá trị thực của x để đồ thị hàm số y = log0,5x nằm phía trên đường thẳng y = 2
![]()
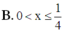
![]()
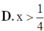
Tìm tất cả các giá trị thực của x để đồ thị hàm số y = log 0 , 5 x nằm phía trên đường thẳng y=2
A. x ≥ 1 4
B. 0 < x ≤ 1 4
C. 0 < x < 1 4
D. x ≥ 1 4
Đáp án C
log 0 , 5 x > 2 ⇔ 0 < x < 1 4 .
Tìm tất cả các giá trị thực của x để đồ thị hàm số y = l o g 0 , 5 x nằm phía trên đường thẳng y = 2
A. x ≥ 1 4
B. 0 < x ≤ 1 4
C. 0 < x < 1 4
D. x > 1 4
Đáp án C
Ta có log 0 , 5 x > 2 ⇔ 0 < x < 1 4 .
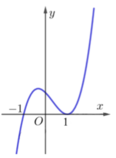
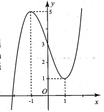
Cho hàm số y=f(x)(x-1) xác định và liên tục trên R và có đồ thị như hình vẽ dưới đây. Tìm tất cả các giá trị thực của tham số m để đường thẳng y = m 2 - m cắt đồ thị hàm số f x x - 1 tại 2 điểm có hoành độ nằm ngoài đoạn [-1;1]
A. m > 0
B. [ m > 1 m < 0
C. m < 1
D. 0 < m < 1
Đáp án B
Lấy đối xứng đồ thị hàm số f(x)(x-1) qua trục Ox ta được đồ thị của hàm số f x x - 1 . Từ đồ thị hàm số f x x - 1 ta thấy đường thẳng y = m 2 - m cắt hàm số f x x - 1 tại 2 điểm nằm ngoài [-1;1]
⇔ m 2 - m > 0 ⇔ [ m < 0 m > 1
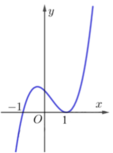
Cho hàm số y = f(x)(x - 1) xác định và liên tục trên ℝ và có đồ thị như hình vẽ dưới đây. Tìm tất cả các giá trị thực của tham số m để đường thẳng y = f x x − 1 cắt đồ thị hàm số tại 2 điểm có hoành độ nằm ngoài đoạn [-1;1]
A. m > 0.
B. m > 1 m < 0 .
C. m < 1.
D. 0 < m < 1.
Đáp án B
Lấy đối xứng đồ thị hàm số f ( x ) ( x − 1 ) qua trục Ox ta được đồ thị của hàm số f ( x ) x − 1 . Từ đồ thị hàm số f ( x ) x − 1 ta thấy đường thẳng y = m 2 − m cắt hàm số f ( x ) x − 1 tại 2 điểm nằm ngoài [ − 1 ; 1 ] ⇔ m 2 − m > 0 ⇔ m < 0 m > 1
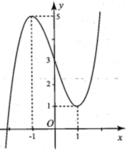
Cho hàm số y=f(x) liên tục trên R, có đồ thị (C) như hình bên. Tìm tất cả các giá trị thực của tham số m để đường thẳng y=2m-1 cắt đồ thị (C) tại 2 điểm phân biệt
A.![]()
B. ![]()
C. ![]()
D. ![]()
Cho hàm số y = f ( x ) liên tục trên R, có đồ thị (C) như hình bên. Tìm tất cả các giá trị thực của tham số m để đường thẳng y = 2 m - 1 cắt đồ thị (C) tại 2 điểm phân biệt
A. m > 3
B. m < 1
C. m = 1 m = 3
D. 1 < m < 3
Tìm tất cả các giá trị của tham số m để đồ thị hàm số y = x 3 + 2 x 2 + m - 3 x + m có 2 điểm cực trị và điểm M(9;-5) nằm trên đường thẳng đi qua hai điểm cực trị của đồ thị hàm số.
A. m = 3
B. m = 2
C. m = -5
D. m = -1
Câu 2: Cho các hàm số bậc nhất \(y=\left(m-2\right)x+2\)
a. Tìm tất cả các giá trị của m để hàm số đã cho đồng biến trên R
b. Tìm tất cả các giá trị của m để đồ thị hàm số đã cho song song với đường thẳng \(y=5x+1\)
a) Để đồ thị hàm số \(y=\left(m-2\right)x+2\) đồng biến trên R.
=> \(m-2>0.\)
<=> \(m>2.\)
b) Đồ thị hàm số \(y=\left(m-2\right)x+2\) song song với đường thẳng \(y=5x+1.\)
=> \(m-2=5.\)
<=> \(m=7.\)
Câu 2
a) Để hs đã cho đồng biến trên R thì:
\(m-2>0\\ < =>m>2\)
b) Đề đths đã cho song song với đường thẳng \(y=5x+1\) thì:
\(m-2=5\\ < =>m=7\)
Tìm tất cả giá trị thực của m để đồ thị hàm số y = 1 3 x 3 - m x 2 + ( 2 m + 1 ) x - 3 có hai cực trị nằm cùng phía với trục tung.
A. m ∈ ( 1 ; + ∞ )
B. m ∈ 1 2 ; 1 ∪ ( 1 ; + ∞ )
C. m ∈ 1 2 ; + ∞
D. m ∈ - ∞ ; 1 2