Một hình trụ có bán kính đáy bằng chiều cao và bằng a. Một hình vuông ABCD có AB;CD là 2 dây cung của 2 đường tròn đáy và mặt phẳng (ABCD) không vuông góc với đáy. Diện tích hình vuông đó bằng .
A. 5 a 2 4
B. 5 a 2 2 4
C. 5 a 2
D. 5 a 2 2
Cho một hình trụ có chiều cao và bán kính đều bằng a. Một hình vuông ABCD có hai cạnh AB, CD lần lượt là hai dây cung của hai đường tròn đáy, cạnh AD, BC không phải là đường sinh của hình trụ. Tính cạnh của hình vuông này
A. a
B. 2a
C. a 5 2
D. a 10 2
Cho một hình trụ có chiều cao và bán kính đều bằng a. Một hình vuông ABCD có hai cạnh AB, CD lần lượt là hai dây cung của hai đường tròn đáy, cạnh AD, BC không phải là đường sinh của hình trụ. Tính cạnh của hình vuông này.
A. a
B. 2a
C. a 10 2
D. a 5 2
Đáp án C
Giả sử dựng được hình vuông ABCD như hình vẽ.

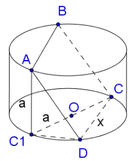
Cho một hình trụ (T) có chiều cao và bán kính đều bằng 3a. Một hình vuông ABCD có hai cạnh AB, CD lần lượt là hai dây cung của hai đường tròn đáy, cạnh AD, BC không phải là đường sinh của hình trụ (T). Tính cạnh của hình vuông này.
![]()
![]()
![]()
Cho một hình trụ (T) có chiều cao và bán kính đều bằng 3a. Một hình vuông ABCD có hai cạnh AB, CD lần lượt là hai dây cung của hai đường tròn đáy, cạnh AD, BC không phải là đường sinh của hình trụ (T). Tính cạnh của hình vuông này.
A. 3 a 5
B. 6 a
C. 3 a 10 2
D. 3 a
Đáp án C
Phương pháp: Gọi là tâm hình vuông ⇒ I ∈ O O ' .
Sử dụng định lý Py-ta-go trong tam giác vuông để tính AB.
Cách giải:
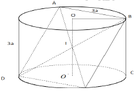
Ta có: I B = O I 2 + O B 2 = 9 a 2 4 + 9 a 2 = 3 a 5 2
⇒ A B = B I . 2 = 3 a 10 2
Cho hình trụ bán kính r và có chiều cao cũng bằng r. Một hình vuông ABCD có hai cạnh AB và CD lần lượt là các dây cung của hai đường tròn đáy, còn cạnh BC và AD không phải là đường sin của hình trụ. Tính diện tích của hình vuông đó và côsin của góc giữa mặt phẳng chứa hình vuông và mặt phẳng đáy ?
Hạ đường sinh AA1 vuông góc với đáy chứa cạnh CD. Khi đó góc ADA1 là góc giữa hai mặt phẳng hình vuông và mặt đáy.
Vì góc A1DC = 1v nên A1C là đường kính.
Gọi cạnh hình vuông là a.
Ta có
a2 = AD2 = AA12 + A1D2
mà AA1 = h = r, nên ta có:
A1D2 + DC2 = A1C2;
a2 – r2 + a2 = 4r2;
⇒a2=52r2
Vậy diện tích hình vuông là: SABC=a2=52r2 Gọi δ = góc ADA1 là góc tạo bởi mặt phẳng hình vuông và đáy, ta có: sinδ = A1AAD=ra=√25Cho một hình trụ có bán kính đáy bằng R và có chiều cao bằng R 3 Hai điểm A,B lần lượt nằm trên hai đường tròn đáy sao cho góc giữa AB và trục của hình trụ bằng 30 ° . Khoảng cách giữa AB và trục của hình trụ bằng:
![]()
![]()
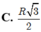
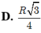
Một hình trụ có chiều cao h = 2 bán kính đáy r = 3.Một mặt phẳng (P) không vuông góc với đáy của hình trụ, lần lượt cắt hai đáy theo các đoạn giao tuyến AB và CD sao cho tứ giác ABCD là hình vuông. Tính diện tích S của hình vuông ABCD.
![]()
![]()
![]()
![]()
Một hình trụ có chiều cao h=2, bán kính đáy r=3. Một mặt phẳng (P) không vuông góc với đáy của hình trụ, lần lượt cắt hai đáy theo các đoạn giao tuyến AB và CD sao cho tứ giác ABCD là hình vuông. Tính diện tích S của hình vuông ABCD
A. S=12ᴨ
B. S=12
C. S=20
D. S=20ᴨ