Cho tứ diện ABCD có tam giác ABD đều cạnh bằng 2, tam giác ABC vuông tại B, B C = 3 . Biết khoảng cách giữa hai đường thẳng chéo nhau AB và CD bằng 11 2 . Khi đó độ dài cạnh CD là
A. 2
B. 2
C. 1
D. 3
Cho tứ diện ABCD có tam giác ABD đều là cạnh bằng 2, tam giác ABC vuông tại B, B C = 3 . Biết khoảng cách giữa hai đường thẳng chéo nhau AB và CD bằng 11 2 . Khi đó độ dài cạnh CD là
A. 2
B. 1
C. 3
D. 2
Phương pháp
+) Dựng E sao cho ABCE là hình bình hành. Chứng minh d(AB;CD) = d(M;(CDE)).
+) Dựng khoảng cách từ M đến (CDE).
+) Áp dụng định lí Pytago trong các tam giác hình vuông tính CD.
Cách giải
Dựng E sao cho ABCE là hình bình hành như hình vẽ.
Cho tứ diện ABCD có tam giác ABD đều cạnh bằng 2, tam giác ABC vuông tại B, B C = 3 . Khoảng cách giữa hai đường thẳng AB và CD bằng 3 2 . Thể tích khối tứ diện ABCD bằng
A. 3 2
B. 1 2
C. 3 6
D. 1 6
Cho tứ diện ABCD có hai mặt ABC và ABD là các tam giác đều. Tính góc giữa hai đường thẳng AB và CD.
A. 30 °
B. 60 °
C. 90 °
D. 120 °
Bài 1: Cho tam giác ABC cân tại A có BC = 4cm. Hai điểm D và E lần lượt nằm trên cạnh AC và AB sao cho AD = 2DC, AE=2EB và BD,Ce vuông góc với nhau. Tính diện tích tam giác ABC.
Bài 2: Cho tứ giác ABCD. Qua trung điểm M của đường chéo BD dựng đường thẳng // AC cắt AD tại E. Chứng minh CE chia tứ giác ABCD thành 2 phần có diện tích bằng nhau.
Cho hình thang \(ABCD\) có hai đáy là \(AB\), \(CD\) và có hai đường chéo bằng nhau (Hình 10). Vẽ đường thẳng đi qua \(C\), song song với \(BD\) và cắt \(AB\) tại \(E\).
a) Tam giác \(CAE\) là tam giác gì? Vì sao?
b) So sánh tam giác \(ABD\) và tam giác \(BAC\)
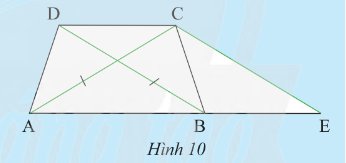
a) Vì \(ABCD\) là hình thang cân (gt)
\( \Rightarrow AC = BD\) và \(AB\;{\rm{//}}\;CD\)
Xét \(\Delta BCD\) và \(\Delta CBE\) ta có:
\(\widehat {DCB} = \widehat {CBE}\) (do \(AB\) // \(CD\))
\(BC\) chung
\(\widehat {CBD} = \widehat {BCE}\) (do \(CE\) // \(BD\))
Suy ra \(\Delta BCD = \Delta CBE\) (g-c-g)
Suy ra \(BD = CE\) (hai cạnh tương ứng)
Mà \(AC = BD\) (cmt)
Suy ra \(AC = EC\)
Suy ra \(\Delta CAE\) cân tại \(C\)
b) Xét \(\Delta ABD\) và \(\Delta BAC\) ta có:
\(DA = BC\) (do \(ABCD\) là hình thang cân)
\(\widehat {DAB} = \widehat {CBA}\) (Do \(ABCD\) là hình thang cân)
\(AB\) chung
Suy ra \(\Delta ABD = \Delta BAC\) (c-g-c)
Cho tứ diện ABCD có AD ⊥ (ABC), ABC là tam giác vuông tại B. Biết
BC=A, AB=a 3 , AD=3a Quay các tam giác ABC và ABD xung quanh đường thẳng AB ta được 2 khối tròn xoay. Thể tích phần chung của 2 khối tròn xoay đó bằng
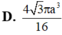
1. Tìm số có 3 chữ số biết rằng số ấy gấp lên 6 lần số tạo nên do ta bỏ chữ số hàng trăm của nó?
2. Cho hình thang ABCD đáy bé bằng 3/4 đáy lớn. Hai đường chéo cắt nhau tại O.
a, Có nhung cặp tam giác nào bằng nhau?
b, so sánh S ABC với S BDC?
c, Cho S ABC bằng 30cm2. Tính S hình thang ABCD
3. Cho tam giác ABC . Trên BC lấy điểm D sao cho BC gấp 3 lần CD. Gọi E là điểm chính giữa cạnh AB . Biết diện tích tứ giác ACDE là 56cm2. Tính diện tích tam giác ABC.
1.Cho hình thang ABCD có hai đáy AB và CD, hai đường chéo cách nhau tại O, biết diện tích tam giác AOB bằng 4 cm2 , diện tích tam giác BOC bằng 9cm2. Tính diện tích hình thang ABCD.
2.Cho hình thang ABCD có hai đường chéo AC và BD cắt nhau tại O và AO bằng 1/2 OC. Diện tích hình tam giác BOC là 12 cm2. Tính diện tích hình thang ABCD?
3.Cho hình thang ABCD. Đáy lớn CD gấp đôi đáy bé AB. Hai đường chéo AC và BD cắt nhau tại G. Biết diện tích tam giác BOC là 34,5 cm2. Tính diện tích hình thang ABCD.
4.Cho hình thang ABCD. Đáy lớn CD, đáy bé AB. Hai đường chéo AC và BD cắt nhau tại G. Biết diện tích tam giác ABG là 34,5 cm2 và diện tích tam giác DGC là 138 cm2. Tính diện tích hình thang ABCD.
[ Làm chi tiết giúp mình nhé!]
