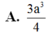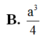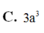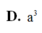Cho hình lăng trụ ABC.A'B'C' có A B = 1 , A C = 2 , C A B ^ = 135 0 , A A ' = 1 . Hình chiếu vuông góc của điểm A trên mặt phẳng (A’B’C’) trùng với trung điểm H của B’C’, Số đo của góc hợp bởi đường thẳng AH và mặt phẳng (ABB’A’) bằng
![]()
![]()
![]()
![]()
a) Cho hình lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông cân tại A, AB=a. Biết diện tích tứ giác ABB'A' bằng \(2a^2\), thể tích khối lăng trụ ABC.A'B'C' bằng?
b) Cho hình lăng trụ đúng ABC.A'B'C' có đáy ABC là tam giác vuông cân tại A, AB=a. Biết góc giữa (AB'C') và (A'B'C') bằng 60°, thể tích khối lăng trụ ABC.A'B'C' bằng?
a: BB'=2a^2:a=2a
V=BB'*S ABC
=2a*1/2a^2
=a^3
Cho lăng trụ đứng tam giác ABC.A'B'C' như hình vẽ a, có đáy là tam giác ABC vuông cân tại B và AC = 5 cm, BB' = 7 cm.
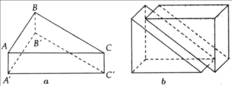
a) Tính diện tích toàn phần của lăng trụ ABC.A’B'C'.
b) Ghép 2 hình lăng trụ đứng có cùng kích thước như lăng trụ đứng ABC.A'B'C' (như hình b). Tính thể tích của hình lăng trụ đứng mới được tạo thành.
Cho hình lăng trụ ABC.A'B'C' có các mặt bên là hình vuông cạnh a 2 . Tính theo a thể tích V của khối lăng trụ ABC.A'B'C'.
A. V = 6 a 3 2
B. V = 3 a 3 12
C. V = 3 a 3 4
D. V = 6 a 3 6
Chọn A.
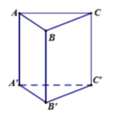
Từ giả thiết suy ra đáy của hình lăng trụ là tam giác đều cạnh bằng 2 a Diện tích của đáy là:
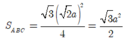
=> Thể tích của lăng trụ là: 
Cho hình lăng trụ đứng ABC.A'B'C' có đáy là tam giác vuông cân tại B, AB = a, A'B=a 3 . Thể tích khối lăng trụ ABC.A'B'C' bằng:
A. a 3 3 2
B. a 3 6
C. a 3 2
D. a 3 2 2
Chọn D.
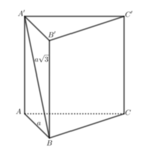
Do tam giác A'AB vuông tại A nên theo pytago ta có
![]()
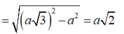
Lại có tam giác ABC vuông cân tại B nên
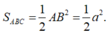
Thể tích khối lăng trụ đã cho
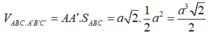
Cho hình lăng trụ đứng ABC.A'B'C' có đáy là tam giác đều cạnh a. Cạnh bên AA'=a 2 . Thể tích khối lăng trụ ABC.A'B'C' là:
A. V = a 3 6 4
B. V = a 3 6 2
C. V = a 3 6 12
D. V = a 6 4
Cho hình lăng trụ đứng ABC.A'B'C' có AA'=2a, tam giác ABC vuông tại B có AB=a; BC=2a. Thể tích khối lăng trụ ABC.A'B'C' là
A. 2 a 3
B. 2 a 3 3
C. 4 a 3 3
D. 4 a 3
Cho hình lăng trụ đứng ABC.A'B'C' có AA' = 2a, tam giác ABC vuông tại B, có AB = a, BC = 2a. Thể tích khối lăng trụ là ABC.A'B'C'
A. 2 a 3
B. 2 a 3 3
C. 4 a 3 3
D. 4 a 3
Một hình lăng trụ đứng ABC.A'B'C'(đáy là tam giác đều ABC) ở bên trong một hình trụ. Các đỉnh A, B, C, A', B', C' thuộc hình trụ. Hình lăng trụ đứng và hình trụ có cùng chiều cao. Cho biết chu vi tam giác ABC là 6cm, thể tích của hình lăng trụ đứng là 123 cm³. Hãy tính chiều cao và thể tích của hình trụ( kết quả làm tròn đến hàng đơn vị)
Chú ý: Thể tích hình trụ đứng = diện tích đáy nhân với chiều cao.
Diện tích tam giác đều là: AB^2√3/4
Thể tích hình trụ = diện tích đáy nhân với chiều cao.
AB=2cm
=>S ABC=căn 3(cm2)
=>h=12(cm)
Cho hình lăng trụ đứng tam giác ABC.A'B'C' có đáy là các tam giác vuông tại B và B', AA' = 5 cm, AB = 2 cm, AC = 6 cm.
a) Tính diện tích xung quanh lăng trụ.
b) Tính diện tích toàn phần lăng trụ.
c) Tính thể tích lăng trụ
a) Diện tích xung quanh của hình lăng trụ là: (2.6):2.5=30(m2) b) Diện tích toàn phần của hình lăng trụ là: 30+2.(2.6):2=42(m2) c) Thể tích của hình lăng trụ là: 5.(2.6):2=30(m3) Đáp số: a) 30m2; b) 42m2; 30m3
Cho hình lăng trụ tam giác đều ABC.A'B'C' có AB=2a, AA'=a 3 . Tính thể tích khối lăng trụ ABC.A'B'C'.