Có bao nhiêu cặp điểm thuộc ( C ) : y = x x - 1 đối xứng nhau qua
Đồ thị hàm số y = x 3 - x + 1 có bao nhiêu cặp điểm M, N đối xứng nhau qua điểm I(0;1)
Tọa độ cặp điểm thuộc đồ thị (C) của hàm số y = x + 4 x - 2 đối xứng nhau qua đường thẳng d: x-2y-6 = 0 là
A.
B. 
C. 
D. 
Đáp án B
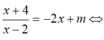
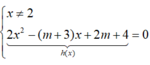
Điều kiện cần:
Để ∆ cắt (C) tại hai điểm phân biệt thì phương trình h(x) = 0 có hai nghiệm phân biệt khác 2, tức là
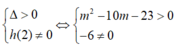
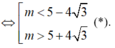
Điều kiện đủ:
Gọi I là trung điểm của AB, ta có:
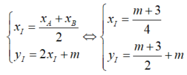
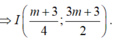
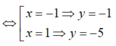
Vậy tọa hai điểm cần tìm là
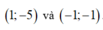
Trên đồ thị (C) của hàm số y = x 3 - 5 x 2 + 6 x + 3 có bao nhiêu cặp điểm đối xứng nhau qua gốc tọa độ
A. 2.
B. 1.
C. 0.
D. 3.
Đáp án A
Gọi 
là hai điểm trên (C) đối xứng nhau qua gốc tọa độ, ta có
Tìm cặp điểm thuộc đồ thị (C) của hàm số y = x + 2 x + 1 đối xứng nhau qua gốc tọa độ.
A. 2 ; 2 và − 2 ; − 2
B. 3 ; − 2 và − 3 ; 2
C. 2 ; − 2 và − 2 ; 2
D. (2;-2và (-2;2)
Đáp án A
Phương pháp: Tham số hóa điểm thuộc đồ thị hàm số (C).
Lấy điểm đối xứng với điểm đó qua O (Điểm (a;) đối xứng với điểm (-a;-b)qua gốc tọa độ O).
Cho điểm đối xứng vừa xác định thuộc (C).
Cách giải:
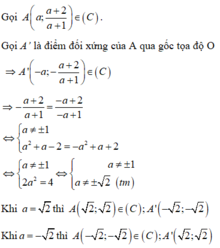
Chú ý và sai lầm : Có thể thử trực tiếp từng đáp án và suy ra kết quả.
1....cho hàm số y=-x3+3x2 -4 (C). Tìm m để đường thẳng d: y=m(x+1) cắt đồ thị (C) tại 3 điểm M(-1;0), B, C sao cho MA=2MB
2....Cho hàm số y=\(\frac{2x}{x+1}\) (C). Tìm 2 điểm thuộc (C) đối xứng qua d: 2x +y - 4 =0
3.... Cho h số y+\(\frac{x^2-2x+2}{x-1}\) (C).Tìm m để đường thẳng d: y= -x +m cắt (C) tại 2 điểm đối xứng nhau qua đường thẳng y = x+3
4. Trong mặt phẳng Oxy, cho đường thẳng d: x − 3y + 1 = 0 và điểm I(−3; 1).
(a) Tìm ảnh của điểm M(1; −2) qua phép đối xứng tâm I.
(b) Tìm ảnh của đường thẳng ∆: 2x + y − 1 = 0 qua phép đối xứng tâm I.
(c) Tìm ảnh của đường tròn (C): (x − 2)2 + (y + 3)2 = 9 qua phép đối xứng
Cho hàm số: y=x-3-3(m+1)x2+9x+m-2 (1) có đồ thị là (Cm). Có bao nhiêu giá trị nguyên của tham số m để (Cm) có điểm cực đại, cực tiểu đối xứng với nhau qua đường thẳng y=1/2x ?
A. 0
B. 1
C. 2
D. 3
Y= -X^3 + 3mx^2-3m-1 có 2 điểm cực trị đối xứng nhau qua x+8y-74=0
Lời giải:
Ta có :
\(y=-x^3+3mx^2-3m-1\)
\(\Rightarrow y'=-3x^2+6mx=0\Leftrightarrow 2mx-x^2=0\)
\(\Leftrightarrow \) \(\left[{}\begin{matrix}x=0\\x=2m\end{matrix}\right.\)
Để ĐTHS có 2 cực trị thì trước tiên \(m\neq 0\)
Khi đó, hai điểm cực trị của ĐTHS là: \(A(0,-3m-1)\) và \(B(2m,4m^3-3m-1)\)
Hai điểm cực trị đối xứng nhau qua \(d: x+8y-74=0\)
\(\Leftrightarrow d(A,d)=d(B,d)\)
\(\Leftrightarrow |0+8(-3m-1)-74|=|2m+8(4m^3-3m-1)-74|\)
\(\Leftrightarrow |-24m-82|=|32m^3-22m-82|\)
Từ đây ta chia ra 2TH:
TH1: \(-24m-82=32m^3-22m-82\)
TH2: \(24m+82=32m^3-22m-82\)
Từ 2 TH ta thu được \(m=2\) thỏa mãn
