Giả sử hàm  f có đạo hàm cấp n trên R, n ∈ ℕ *  và f 1 - x + x 2 f   ' ' x = 2 x  với mọi x ∈ ℝ . Tính tích phân ∫ 0 1 x f ' x d x   

A. I = 1  

B. I = - 1  

C. I = 1 3  

D. I = - 1 3  

Giả sử hàm số f có đạo hàm cấp n trên R thỏa mãn f 1 - x + x 2 f ' ' x = 2 x với mọi x ∈ R . Tính tích phân I = ∫ 0 1 xf ' x dx .

A. I = 1

B. I = 2

C. I = 1/3

D. I = 2/3

Giả sử hàm f có đạo hàm cấp 2 trên R thỏa mãn f 1 = f ' 1 = 1 và f 1 - x + x 2 f ' ' x = 2 x ,   ∀ x ∈ ℝ . Tính tích phân  ∫ 0 1 x f ' x d x

A. I = 1

B. I = 2

C.  I = 1 3

D. I = 2 3

Xét các khẳng định sau

i) Nếu hàm số y=f(x) có đạo hàm cấp hai trên R và đạt cực tiểu tại x = x 0  thì  f ' x 0 = 0 f ' ' x 0 > 0

ii) Nếu hàm số y=f(x) có đạo hàm cấp hai trên R và đạt cực đại tại x = x 0  thì f ' x 0 = 0 f ' ' x 0 < 0

iii) Nếu hàm số y=f(x) có đạo hàm cấp hai trên R và f ' ' x 0 = 0  thì hàm số không đạt cực trị tại  x = x 0

Số khẳng định đúng trong các khẳng định trên là

A. 0

B. 1

C. 2

D. 3

Cho hàm số f (x) có đạo hàm cấp 3 xác định và liên tục trên R thoả mãn f(x)f‴(x) = x ( x 2 - 1 ) ( x - 4 ) , ∀ x ∈ R . Hàm số  g ( x ) = ( f ' ( x ) ) 2 - 2 f ( x ) f '' ( x ) đồng biến trên khoảng nào ?

A. (0;1).

B. (-1;0).

C. ( 4 ; + ∞ ) .

D. ( - ∞ ; - 1 ) .

Cho hàm số y=f(x) liên tục trên R có đạo hàm cấp 3 với f’’’(x)=0 và thỏa mãn f ( x ) ' 2018 1 - f ' ' ( x )   =   2 x ( x + 1 ) 2 ( x - 2018 ) 2019 :   f ' ' ( x ) ,   ∀ x ∈ R  Hàm số g ( x )   =   f ' ( x ) 2019 1 - f ' ' ( x )  có bao nhiêu điểm cực trị?

A. 1

B.2

C.3

D. 4 

Cho hàm số y = f(x) liên tục và có đạo hàm cấp hai trên R. Đồ thị của các hàm số y = f(x), y = f'(x) và y = f''(x) lần lượt là các đường cong nào trong hình vẽ bên. 

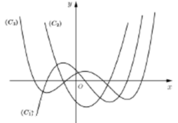
A.  C 1 ,   C 3 ,   C 2

B. C 3 ,   C 2 ,   C 1

C. C 3 ,   C 1 ,   C 2

D. C 1 ,   C 2 ,   C 3

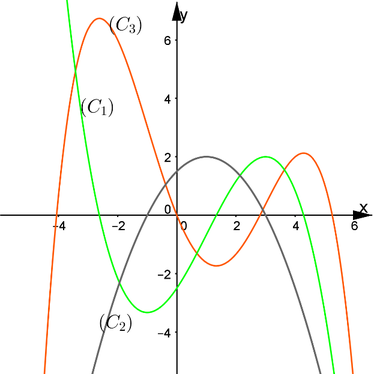
Cho hàm số y=f(x) liên tục và có đạo hàm cấp hai trên R. Đồ thị của các hàm số y=f(x),y=f '(x),y=f ''(x) lần lượt là đường cong nào trong hình bên?

.

A. .

B. .

C. .

D. .

Cho hàm số y=f(x) liên tục và có đạo hàm cấp hai trên R. Đồ thị của các hàm số y=f(x), y=f'(x), y=f''(x) lần lượt là các đường cong nào trong hình vẽ bên.

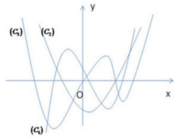
A. C 3 ,   C 1 ,   C 2

B. C 1 ,   C 2 ,   C 3

C. C 3 ,   C 2 ,   C 1

D.  C 1 ,   C 3 ,   C 2