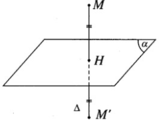
Tìm tọa độ hình chiếu vuông góc H của điểm M(1; 2; -4) trên trục Oz
A. H(0;2;0)
B. H(1;0;0)
C. H(0;0;–4)
D. H(1;2;–4)
Tìm tọa độ điểm H là hình chiếu vuông góc của điểm M(1; -1; 2) trên mặt phẳng (α): 2x – y + 2z + 11 = 0.
Vecto pháp tuyến của mp α là n → =(2;-1;2), H là hình chiếu vuông góc của M trên mp α nên M H ⊥ m p α , đường thẳng MK có vecto pháp tuyến n → = ( 2 ; - 1 ; 2 )
Ta có pt tham số của đường thẳng MH là : x = 1 + 2 t y = - 1 - t z = 2 + 2 t
Thay x,y,z từ pt tham số của đường thẳng MH và pt mp α , ta có:
2(1+2t)-(-1-t)+2(2+2t)+11=0 <=> t=-2
Vậy H(-3;1;-2)
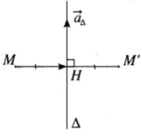
Cho điểm M(2; -1; 1) và đường thẳng
∆ : x - 1 2 = y + 1 - 1 = z 2
Tìm tọa độ điểm H là hình chiếu vuông góc của điểm M trên đường thẳng ∆
Phương trình tham số của
∆
: 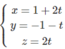
Xét điểm H(1 + 2t; −1 − t; 2t) ∈ ∆
Ta có MH → = (2t − 1; −t; 2t − 1)
a ∆ → = (2; −1; 2)
H là hình chiếu vuông góc của M trên ∆ ⇔ MH → . a ∆ → = 0
⇔ 2(2t − 1) + t + 2(2t − 1) = 0 ⇔ t = 4/9
Ta suy ra tọa độ điểm 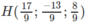
cho điểm m (-1 1) và đường thẳng denta 3x+y-8=0
a)Viết phương trình đường thẳng d đi qua m vuông góc với đường thẳng denta
b)Tìm tọa độ hình chiếu vuông góc với h của điểm M lên đường thẳng delta
c)tọa độ điểm M' đối xứng với điểm M Qua denta
a.
Do d vuông góc với \(\Delta\) nên d nhận \(\left(1;-3\right)\) là 1 vtpt
Phương trình d:
\(1\left(x+1\right)-3\left(y-1\right)=0\Leftrightarrow x-3y+4=0\)
b.
\(M\in d\) mà \(MH\perp\Delta\Rightarrow\) H là giao điểm của d và \(\Delta\)
Tọa độ H là nghiệm của hệ:
\(\left\{{}\begin{matrix}x-3y+4=0\\3x+y-8=0\end{matrix}\right.\) \(\Rightarrow H\left(2;2\right)\)
c.
M' đối xứng với M qua \(\Delta\) khi và chỉ khi H là trung điểm MM'
Theo công thức trung điểm:
\(\left\{{}\begin{matrix}x_{M'}=2x_H-x_M=5\\y_{M'}=2y_H-y_M=3\end{matrix}\right.\) \(\Rightarrow M'\left(5;3\right)\)
Tại sao lại đổi từ (3; 1) sang (1; -3 ) vậy ạ? Denlta có dạng pttq thì có vtpt và đường thẳng d cũng vuông góc với denlta rồi mà?
Trong không gian với hệ tọa độ Oxyz, gọi H hình chiếu vuông góc của M(2;0;1) lên đường thẳng ∆ : x - 1 1 = y 2 = z - 2 1 . Tìm tọa độ điểm H .
A. H(2;2;3)
B. H(0;-2;1)
C. H(1;0;2)
D. H(-1;-4;0)
Đáp án C.
Vtcp của ∆ là: u → = ( 1 ; 2 ; 1 ) . Phương trình mặt phẳng qua M và nhận u → = ( 1 ; 2 ; 1 ) làm vtpt là:
![]()
![]()
![]()
=> tọa độ của H là nghiệm của hệ phương trình
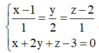
![]()
Cho điểm M(1; -1; 2) và mặt phẳng ( α ): 2x – y + 2z + 12 = 0. Tìm tọa độ điểm H là hình chiếu vuông góc của điểm M trên mặt phẳng ( α )
Phương trình tham số của đường thẳng ∆ đi qua điểm M(1; -1; 2) và vuông góc với mặt phẳng ( α ): 2x – y + 2z + 12 = 0 là:
Δ 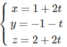
Xét điểm H(1 + 2t; -1 – t; 2 + 2t) ∈ ∆
Ta có H ∈ ( α ) ⇔ 2(1 + 2t) + (1 + t) + 2(2 + 2t) + 12 = 0 ⇔ t = −19/9
Vậy ta được ![]()
Cho điểm M(1; 4; 2) và mặt phẳng (α): x + y + z – 1 = 0 Tìm tọa độ điểm H là hình chiếu vuông góc của điểm M trên mặt phẳng (α).
Đường thẳng MH vuông góc với (α)
⇒ MH nhận vtpt của (α) 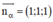 là 1 vtcp
là 1 vtcp
Mà M(1; 4; 2) ∈ MH
⇒ Pt đường thẳng MH: 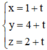
⇒ H(1 + t; 4 + t; 2 + t).
H ∈ (α) ⇒ 1 + t + 4 + t + 2 + t – 1 = 0 ⇔ t = -2.
⇒ H(-1; 2; 0).
1.Cho điểm M(1 ; 4 ; 5) và mặt phẳng (α): x + y + z -1 =0. Tìm tọa độ điểm H là hình chiếu vuông góc của điểm M trên mặt phẳng (α).
Lớn rồi có ý thức chút đi buff sp bị người khác phát hiện mà cứ cố cãi làm gì
Trong không gian với hệ tọa độ Oxyz, cho điểm M (2;–1;3) và mặt phẳng (P) có phương trình x – 2 y + z – 1 = 0 . Tìm tọa độ hình chiếu vuông góc H của M trên (P).
A. H = (1;–2;1)
B. H = (1;1;2)
C. H = (3;2;0)
D. H = (4;–2;–3)
Đáp án là B
Phương trình đường thẳng d đi qua M vuông góc
với (P) nhận véc tơ pháp tuyến

Trong không gian với hệ tọa độ Oxyz, cho điểm M (2;–1;3) và mặt phẳng (P) có phương trình x – 2y + z – 1 = 0. Tìm tọa độ hình chiếu vuông góc H của M trên (P).
A. H = (1;–2;1)
B. H = (1;1;2)
C. H = (1;1;2)
D. H = (4;–2;–3)