Tính thể tích V của khối cầu ngoại tiếp hình lập phương cạnh a
A. V = πa 3
B. V = 4 πa 3 3
C. V = 2 πa 3 3
D. V = 3 πa 3 2
Cho hình chóp S.ABC đáy ABC là tam giác vuông tại C, có cạnh AB a = , cạnh bên SA vuông góc mặt phẳng đáy và SA a = 3 . Tính thể tích V khối cầu ngoại tiếp hình chóp.
A. V= 2 2 3 3 a .
B. V= 3 4a .
C. V= 32 3 3 πa .
D. V= 4 3 3 πa .
Tính thể tích V của khối cầu ngoại tiếp hình lập phương cạnh a.
![]()
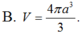
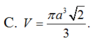
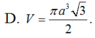
Tính thể tích của khối cầu ngoại tiếp hình lập phương cạnh a bằng
A. πa 3
B. 4 πa 3 3
C. πa 3 3 3
D. πa 3 3 2
Một khối trụ có hai đáy là hai hình tròn ngoại tiếp hai mặt của một hình lập phương cạnh a. Tính theo a thể tích V của khối trụ đó
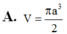
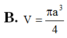
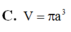

Một khối trụ có hai đáy là hai hình tròn ngoại tiếp hai mặt của một hình lập phương cạnh a. Tính theo a thể tích V của khối trụ đó
A. V = π a 3 2
B. V = π a 3 4
C. V = π a 3
D. V = 2 π a 3
Tính thể tích khối cầu ngoại tiếp hình lập phương có cạnh bằng a
A. V = πa 3 3 2
B. V = 4 πa 3 3
C. V = πa 3 3 8
D. V = 4 πa 3 3 3
A
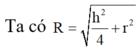
Trong đó R là bán kính khối cầu, h là chiều cao hình lập phương, r là bán kính đuờng tròn ngoại tiếp đáy.
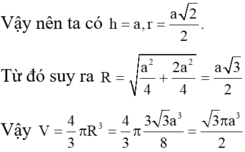
Tính thể tích V của khối cầu tiếp xúc với tất cả các cạnh của hình lập phương cạnh 2 2
A. V = 32 π 3
B. V = 32 π 6
C. V = 256 π 6
D. V = 64 π 2 3
Cho hình lập phương ABCD.A'B'C'D'
có cạnh a. Thể tích khối cầu ngoại tiếp
hình lập phương là
![]()
![]()
![]()
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy là a và cạnh bên là 2a. Tính thể tích V của khối cầu ngoại tiếp hình chóp S.ABCD
A. 16 a 3 π 14 49
B. 64 a 3 π 14 49
C. 64 a 3 π 14 147
D. 2 a 3 π 14 7
Gọi O là tâm hình vuông ABCD,M là trung điểm của SA
Mặt phẳng trung trực của đoạn thẳng SA cắt SO tại I
Điểm I là tâm của mặt cầu ngoại tiếp hình chóp S.ABCD bán kính R=IS
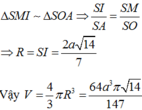
Đáp án C