Các câu hỏi tương tự
Cho hình phẳng D giới hạn bởi đường cong
y
3
+
x
−
2
e
x
x
e
x
+
1
, trục hoành và hai đường th...
Đọc tiếp
Cho hình phẳng D giới hạn bởi đường cong y = 3 + x − 2 e x x e x + 1 , trục hoành và hai đường thẳng x=0, x=1. Khối tròn xoay tạo thành khi quay D quanh trục hoành có thể tích V = π a + b ln 1 + 1 e , trong đó a, b là các số hữu tỷ. Mệnh đề nào dưới đây là đúng?
A. a+b=5
B. a-2b=5
C. a+b=3
D. a-2b=7
Có
∫
0
π
4
cos
x
sin
x
+
cos
x
d
x
π
a
+
1
b
ln
c
với
a
,
b
,
c
∈
ℤ
thì
a
2
+
b
+
c
là: A. 14 B. 66 C...
Đọc tiếp
Có ∫ 0 π 4 cos x sin x + cos x d x = π a + 1 b ln c với a , b , c ∈ ℤ thì a 2 + b + c là:
A. 14
B. 66
C. 66 + 2
D. 70
Cho phương trình sau:
sin
3
x
-
sin
x
+
cos
2
x
1
. Phương trình có họ nghiệm
x
π
a
+
k
2
π
3
,
k
∈
ℤ
hỏi giá trị của a A. 1 B. 6 C. 3 D. 4
Đọc tiếp
Cho phương trình sau: sin 3 x - sin x + cos 2 x = 1 . Phương trình có họ nghiệm x = π a + k 2 π 3 , k ∈ ℤ hỏi giá trị của a
A. 1
B. 6
C. 3
D. 4
Tính thể tích khối cầu ngoại tiếp hình lập phương có cạnh bằng a A.
V
πa
3
3
2
B.
V
4
πa
3
3
C.
V
πa...
Đọc tiếp
Tính thể tích khối cầu ngoại tiếp hình lập phương có cạnh bằng a
A. V = πa 3 3 2
B. V = 4 πa 3 3
C. V = πa 3 3 8
D. V = 4 πa 3 3 3
Tính thể tích V của khối cầu ngoại tiếp hình lập phương cạnh a A.
V
πa
3
B.
V
4
πa
3
3
C.
V
2
πa
3
3
D.
V
3...
Đọc tiếp
Tính thể tích V của khối cầu ngoại tiếp hình lập phương cạnh a
A. V = πa 3
B. V = 4 πa 3 3
C. V = 2 πa 3 3
D. V = 3 πa 3 2
Một khối đa diện (H) được tạo thành bằng cách từ một khối lập phương cạnh bằng 3, ta bỏ đi khối lập phương cạnh bằng 1 ở một “góc” của nó như hình vẽ. Gọi (S) là khối cầu có thể tích lớn nhất chứa trong (H) và tiếp xúc với các mặt (ABCD),(BCCB),(DCCD). Tính bán kính của (S). A.
2
+
3
3
B.
3
-
3
C.
2...
Đọc tiếp
Một khối đa diện (H) được tạo thành bằng cách từ một khối lập phương cạnh bằng 3, ta bỏ đi khối lập phương cạnh bằng 1 ở một “góc” của nó như hình vẽ. Gọi (S) là khối cầu có thể tích lớn nhất chứa trong (H) và tiếp xúc với các mặt (A'B'C'D'),(BCC'B'),(DCC'D'). Tính bán kính của (S).
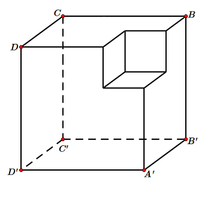
A. 2 + 3 3
B. 3 - 3
C. 2 3 3
D. 2
Một hình lập phương cạnh bằng a nội tiếp khối cầu
S
1
và ngoại tiếp khối cầu
S
2
, gọi
V
1
và
V
2
lần lượt là thể tích của các khối
S
1
và
S
2
. Tính tỉ số
k...
Đọc tiếp
Một hình lập phương cạnh bằng a nội tiếp khối cầu S 1 và ngoại tiếp khối cầu S 2 , gọi V 1 và V 2 lần lượt là thể tích của các khối S 1 và S 2 . Tính tỉ số k = V 1 V 2 .
A. k = 1 2 2
B. k = 1 3 3
C. k = 2 2
D. 3 3
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB 3, AD 4 và các cạnh bên của hình chóp tạo với mặt đáy một góc 600. Tính thể tích của khối cầu ngoại tiếp hình chóp đã cho A.
V
250
3
3
π
B.
V
125...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB = 3, AD = 4 và các cạnh bên của hình chóp tạo với mặt đáy một góc 600. Tính thể tích của khối cầu ngoại tiếp hình chóp đã cho
A. V = 250 3 3 π
B. V = 125 3 6 π
C. V = 500 3 27 π
D. V = 50 3 27 π
Cho hình lập phương có cạnh bằng a. Tính theo a thể tích của khối cầu tiếp xúc với 12 cạnh của hình lập phương đó. A.
π
a
3
6
B.
4
π
a
3
3
C.
π
2
a
3...
Đọc tiếp
Cho hình lập phương có cạnh bằng a. Tính theo a thể tích của khối cầu tiếp xúc với 12 cạnh của hình lập phương đó.
A. π a 3 6
B. 4 π a 3 3
C. π 2 a 3 3
D. π 3 a 3 2



