Tính thể tích của khối lập phương ABCD.A’B’C’D’ cạnh a.
Những câu hỏi liên quan
Tính thể tích của khối lập phương
A
B
C
D
.
A
’
B
’
C
’
D
’
cạnh a. A.
a
3
3
B.
a
3
2
C.
a
3
D.
a
3
6
Đọc tiếp
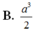
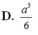
Tính thể tích của khối lập phương A B C D . A ’ B ’ C ’ D ’ cạnh a.
A. a 3 3
B. a 3 2
C. a 3
D. a 3 6
Cho khối lập phương ABCD.A’B’C’D’ có cạnh là a. Tính thể tích khối chóp tứ giác D.ABCD A.
a
3
3
B.
a
3
2
6
C.
a
3
2
3...
Đọc tiếp
Cho khối lập phương ABCD.A’B’C’D’ có cạnh là a. Tính thể tích khối chóp tứ giác D.ABC'D'
A. a 3 3
B. a 3 2 6
C. a 3 2 3
D. a 3 4
Cho hình lập phương ABCD.A’B’C’D’ cạnh bằng a. Tính thể tích khối tứ diện A’C’BD bằng A.
a
3
2
.
B.
a
3
3
.
C.
a
3
3
2
.
D.
a
3...
Đọc tiếp
Cho hình lập phương ABCD.A’B’C’D’ cạnh bằng a. Tính thể tích khối tứ diện A’C’BD bằng
A. a 3 2 .
B. a 3 3 .
C. a 3 3 2 .
D. a 3 2 3 .
Cho hình lập phương ABCD.A’B’C’D’ cạnh bằng a. Tính thể tích khối tứ diện A’C’BD bằng:
A
.
a
3
2
B
.
a
3
3
C
.
a
3
3
2
D...
Đọc tiếp
Cho hình lập phương ABCD.A’B’C’D’ cạnh bằng a. Tính thể tích khối tứ diện A’C’BD bằng:
A . a 3 2
B . a 3 3
C . a 3 3 2
D . a 3 2 3
Cho ABCD.A’B’C’D’ là hình lập phương cạnh 2a. Tính thể tích khối tứ diện ACD’B’ là A.
4
a
3
3
B.
8
a
3
3
C.
2
a
3
3
D.
8...
Đọc tiếp
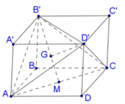
Cho ABCD.A’B’C’D’ là hình lập phương cạnh 2a. Tính thể tích khối tứ diện ACD’B’ là
A. 4 a 3 3
B. 8 a 3 3
C. 2 a 3 3
D. 8 a 3 9
Đáp án B
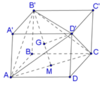
Nhận thấy chóp ACD’B’ có tất cả các cạnh bằng nhau và bằng 2 2 a
Gọi M là trung điểm của AC, G là trọng tâm của tam giác AB’C’. Chóp ACD’B’ nhận D’G là đường cao.
Xét tam giác AB’C’ có
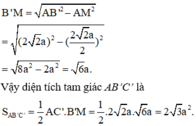
Xét tam giác vuông D’GB’ ta có
Đúng 0
Bình luận (0)
Cho ABCD.A’B’C’D’ là hình lập phương cạnh 2a. Tính thể tích khối tứ diện ACD’B’ là
Đọc tiếp
Cho ABCD.A’B’C’D’ là hình lập phương cạnh 2a. Tính thể tích khối tứ diện ACD’B’ là
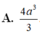
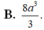
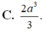
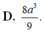
Chọn B
Nhận thấy chóp ACD’B’ có tất cả các cạnh bằng nhau và bằng 2 2 a
Gọi M là trung điểm của AC, G là trọng tâm của tam giác AB’C’. Chóp ACD’B’ nhận D’G là đường cao.
Xét tam giác AB’C’ có
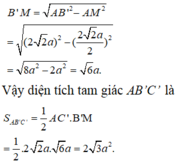
Xét tam giác vuông D’GB’ ta có
Đúng 0
Bình luận (0)
Tính thể tích V của khối lập phương ABCD.A’B’C’D’ biết AC a
3
A
.
V
a
3
B
.
V
a
3
4
C
.
V
3
6...
Đọc tiếp
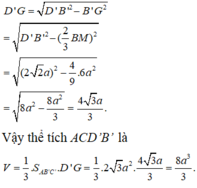
Tính thể tích V của khối lập phương ABCD.A’B’C’D’ biết AC' = a 3
A . V = a 3
B . V = a 3 4
C . V = 3 6 a 3 4
D . V = 3 3 a 3
Đáp án A
Giả sử cạnh của hình lập phương là a. Khi đó AB' = x
2
. Xét tam giác vuông AB’C’ vuông tại B’ ta có 
.
Do đó 
Đúng 0
Bình luận (0)
Cho hình lập phương ABCD.A’B’C’D’ cạnh a. Gọi M là trung điểm A’B’, N là trung điểm BC.
Tính thể tích khối tứ diện ADMN
Cho hình lập phương ABCD.A’B’C’D’ cạnh a. Tính diện tích xung quanh của hình trụ và thể tích của khối trụ có hai đáy là hai hình tròn ngoại tiếp hai hình vuông ABCD và A’B’C’D’.
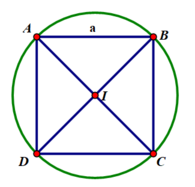
Biểu diễn đường tròn ngoại tiếp hình vuông ABCD cạnh a như hình vẽ
Khi đó: Tâm đường tròn là giao điểm 2 đường chéo
Đúng 0
Bình luận (0)