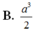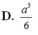Các câu hỏi tương tự
Cho hình lập phương ABCD.A’B’C’D’ cạnh bằng a. Tính thể tích khối tứ diện A’C’BD bằng A.
a
3
2
.
B.
a
3
3
.
C.
a
3
3
2
.
D.
a
3...
Đọc tiếp
Cho hình lập phương ABCD.A’B’C’D’ cạnh bằng a. Tính thể tích khối tứ diện A’C’BD bằng
A. a 3 2 .
B. a 3 3 .
C. a 3 3 2 .
D. a 3 2 3 .
Cho ABCD.A’B’C’D’ là hình lập phương cạnh 2a. Tính thể tích khối tứ diện ACD’B’ là
Đọc tiếp
Cho ABCD.A’B’C’D’ là hình lập phương cạnh 2a. Tính thể tích khối tứ diện ACD’B’ là
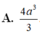
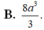
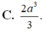
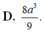
Cho hình lập phương ABCD.A’B’C’D’ cạnh a. Gọi M là trung điểm A’B’, N là trung điểm BC.
Tính thể tích khối tứ diện ADMN
Cho hình lập phương ABCD.A’B’C’D’ cạnh a. Tính diện tích xung quanh của hình trụ và thể tích của khối trụ có hai đáy là hai hình tròn ngoại tiếp hai hình vuông ABCD và A’B’C’D’.
Cho khối lập phương ABCD.A’B’C’D’ cạnh bằng a. Các điểm E và F lần lượt là trung điểm của C’B’ và C’D’. Mặt phẳng (AEF) cắt khối lập phương đã cho thành hai phần, gọi
V
1
là thể tích khối chứa điểm A’ và
V
2
là thể tích khối chứa điểm C’. Khi đó
V
1
V
2
là A.
25
47...
Đọc tiếp
Cho khối lập phương ABCD.A’B’C’D’ cạnh bằng a. Các điểm E và F lần lượt là trung điểm của C’B’ và C’D’. Mặt phẳng (AEF) cắt khối lập phương đã cho thành hai phần, gọi V 1 là thể tích khối chứa điểm A’ và V 2 là thể tích khối chứa điểm C’. Khi đó V 1 V 2 là
A. 25 47 .
B. 1
C. 17 25 .
D. 8 17 .
Cho hình lập phương ABCD.A’B’C’D’ cạnh bằng 2a. Một hình trụ có hai đáy là hai hình tròn nội tiếp trong hai hình vuông ABCD và A’B’C’D’. Tính thể tích của khối lăng trụ tạo nên từ hình trụ trên. A.
2
π
a
3
.
B.
π
a
3
.
C.
2
2
π
a
3
.
D.
4
π
a...
Đọc tiếp
Cho hình lập phương ABCD.A’B’C’D’ cạnh bằng 2a. Một hình trụ có hai đáy là hai hình tròn nội tiếp trong hai hình vuông ABCD và A’B’C’D’. Tính thể tích của khối lăng trụ tạo nên từ hình trụ trên.
A. 2 π a 3 .
B. π a 3 .
C. 2 2 π a 3 .
D. 4 π a 3 .
Cho hình lập phương ABCD.A’B’C’D’ cạnh a. Tính diện tích mặt cầu đi qua tất cả các đỉnh của hình lập phương.
Cho hình lập phương ABCD.A’B’C’D’ cạnh a. Tính diện tích xung quanh
S
x
q
của khối nón có đỉnh là tâm hình vuông A’B’C’D’ và có đường tròn đáy ngoại tiếp hình vuông ABCD
Đọc tiếp
Cho hình lập phương ABCD.A’B’C’D’ cạnh a. Tính diện tích xung quanh S x q của khối nón có đỉnh là tâm hình vuông A’B’C’D’ và có đường tròn đáy ngoại tiếp hình vuông ABCD
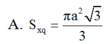
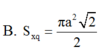
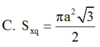
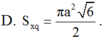
Gọi V là thể tích của khối lập phương ABCD.A’B’C’D’, V1 là thể tích của khối tứ diện A’ABD. Hệ thức nào sau đây là đúng?
Đọc tiếp
Gọi V là thể tích của khối lập phương ABCD.A’B’C’D’, V1 là thể tích của khối tứ diện A’ABD. Hệ thức nào sau đây là đúng?
![]()
![]()
![]()
![]()