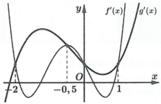
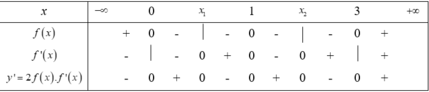
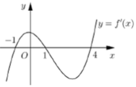
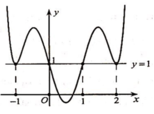
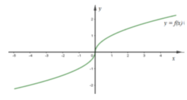
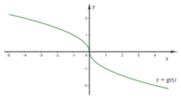
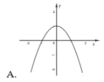
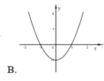
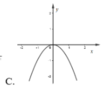
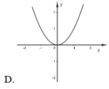
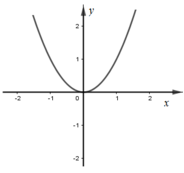
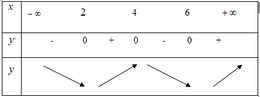
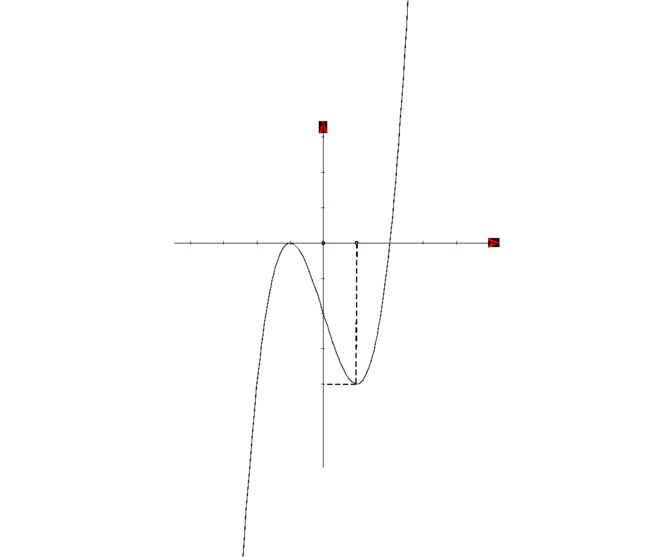
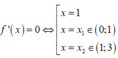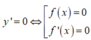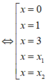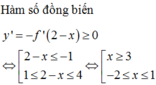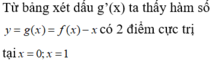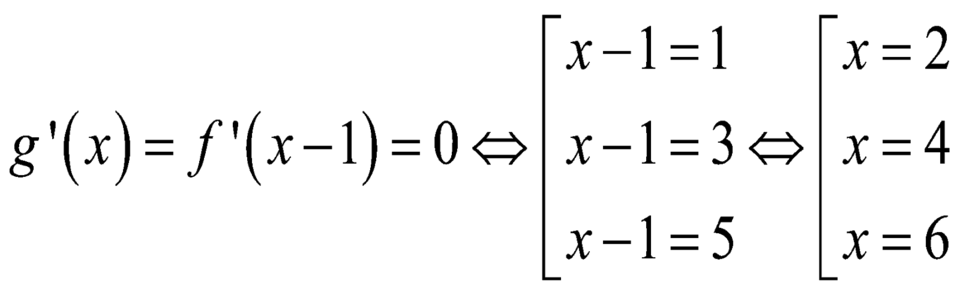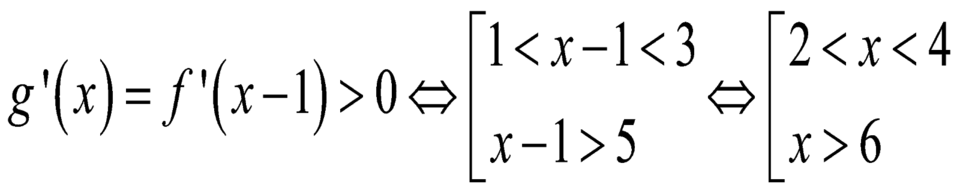Cho hàm sốy = f(x). Hàm số y = f’(x) có đồ thị như hình vẽ dưới đây.
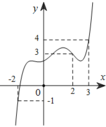
Đặt g x = 2 f x - x + 1 2 .Biết f(-2) = =f(3). Mệnh đề nào đúng?
A. m a x - 2 ; 3 g x = g 3 , m i n - 2 ; 3 g x = g - 2
B. m a x - 2 ; 3 g x = g 2 , m i n - 2 ; 3 g x = g 3
C. m a x - 2 ; 3 g x = g 2 , m i n - 2 ; 3 g x = g - 2
D. m a x - 2 ; 3 g x = g - 2 , m i n - 2 ; 3 g x = g 2