Họ nguyên hàm của hàm số f(x)=sinx+xlnx là:
Những câu hỏi liên quan
Họ nguyên hàm của hàm số
f
(
x
)
sin
x
+
x
ln
x
là A.
F
(
x
)
-
c
o
s
x
+
x
2
2
l
n
x
-
x
2
4
+
C
B. ...
Đọc tiếp
Họ nguyên hàm của hàm số f ( x ) = sin x + x ln x là
A. F ( x ) = - c o s x + x 2 2 l n x - x 2 4 + C
B. F ( x ) = - c o s x + l n x + C
C. F ( x ) = c o s x + x 2 2 l n x - x 2 4 + C
D. F ( x ) = - c o s x + C
Họ các nguyên hàm F(x) của hàm số
f
x
xlnx
trên khoảng
0
;
+
∞
là A.
1
2
x
2
lnx
+
1
4
x...
Đọc tiếp
Họ các nguyên hàm F(x) của hàm số f x = xlnx trên khoảng 0 ; + ∞ là
A. 1 2 x 2 lnx + 1 4 x 2 + C
B. 1 2 x 2 lnx + 1 2 x 2 + C
C. 1 2 x 2 lnx − 1 4 x 2 + C
D. 1 2 x 2 lnx − 1 2 x 2 + C
Họ nguyên hàm của hàm số f(x) = sinx + 1 là
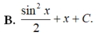
Họ các nguyên hàm của hàm số f(x) = 3 x 2 + s i n x là
A. 6x+cosx+C.
B. x 3 +cosx+C.
C. 6x-cosx+C.
D. x 3 -cosx+C.
Họ các nguyên hàm của hàm số f(x)
(
sin
x
+
cos
x
)
2
là
Đọc tiếp
Họ các nguyên hàm của hàm số f(x)= ( sin x + cos x ) 2 là
Tìm họ nguyên hàm F (x) của hàm số f (x) 3
sin
x
+
2
x
A. F(x)
-
3
cos
x
+
2
ln
x
+
C
B.
F
(
x
)
3
cos
x
+
2...
Đọc tiếp
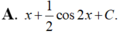
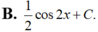
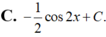
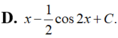
Tìm họ nguyên hàm F (x) của hàm số f (x) = 3 sin x + 2 x
A. F(x) = - 3 cos x + 2 ln x + C
B. F ( x ) = 3 cos x + 2 ln x + C
C. F ( x ) = 3 cos x - 2 ln x + C
D. F ( x ) = - 3 cos x - 2 ln x + C
Họ nguyên hàm của hàm số
f
(
x
)
sin
x
-
4
x
3
Đọc tiếp
Họ nguyên hàm của hàm số f ( x ) = sin x - 4 x 3
Cho
F
(
x
)
là nguyên hàm của hàm số
f
(
x
)
x
ln
x
Tìm
F
(
x
)
A
.
F
(
x
)
1
-
ln
x
B
.
F
(
x
)...
Đọc tiếp
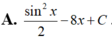
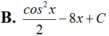
Cho F ( x ) là nguyên hàm của hàm số f ( x ) = x ln x Tìm F ' ' ( x )
A . F ' ' ( x ) = 1 - ln x
B . F ' ' ( x ) = 1 x
C . F ' ' ( x ) = 1 + ln x
D . F ' ' ( x ) = x - ln x
Cho F(x) là một nguyên hàm của hàm số
f
(
x
)
x
ln
x
.
Tính F’’(x)? A.
F
’
’
(
x
)
1
-
ln
x
B.
F
’
’
(
x
)
1
x
C.
F
’
’
(
x
)
1...
Đọc tiếp
Cho F(x) là một nguyên hàm của hàm số f ( x ) = x ln x . Tính F’’(x)?
A. F ’ ’ ( x ) = 1 - ln x
B. F ’ ’ ( x ) = 1 x
C. F ’ ’ ( x ) = 1 + l n x
D. F ’ ’ ( x ) = x + ln x
