Viết phương trình mặt phẳng (P) tiếp xúc với mặt cầu x 2 + y 2 + z 2 - 10 x + 2 y + 26 z + 170 = 0 .Và song song với hai đường thẳng a : x = - 5 + 2 t y = 1 - 3 t z = - 13 + 2 t , a ' : x = - 7 + 3 t ' y = - 1 - 2 t ' z = 8
Những câu hỏi liên quan
Viết phương trình mặt phẳng tiếp xúc với mặt cầu
(
S
)
:
(
x
-
2
)
2
+
(
y
+
1
)
2
+
(
z
-
3
)...
Đọc tiếp
Viết phương trình mặt phẳng tiếp xúc với mặt cầu ( S ) : ( x - 2 ) 2 + ( y + 1 ) 2 + ( z - 3 ) 2 = 9 tại điểm M(6; -2; 3).
A. 4x-y-26=0
B. 4x+y-26=0
C. 4x+y+26=0
D. 4x-y+26=0
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S): \(x^2+y^2+z^2-2x+6y-8z-10=0\) và mặt phẳng (P): \(x+2y-2z=0\). Viết phương trình mặt phẳng (Q) song song với (P) và tiếp xúc với (S).
Trong không gian Oxyz, cho mặt cầu (S):
x
-
1
2
+
y
+
2
2
+
(
z
-
5
)
2
9
. Phương trình nào dưới đây là phương trình mặt phẳng (P...
Đọc tiếp
Trong không gian Oxyz, cho mặt cầu (S): x - 1 2 + y + 2 2 + ( z - 5 ) 2 = 9 . Phương trình nào dưới đây là phương trình mặt phẳng (P) tiếp xúc với mặt cầu (S) tại điểm A(2;-4;3)?
A. x – 6y + 8z – 50 = 0
B. x – 2y – 2z – 4 = 0
C. x – 2y – 2z + 4 = 0
D. 3x – 6y + 8z – 54 = 0
Mặt phẳng tiếp xúc với mặt cầu
(
x
-
2
)
2
+
(
y
+
1
)
2
+
(
z
-
3
)
2
9
tại điểm M(6;-2;3) có phư...
Đọc tiếp
Mặt phẳng tiếp xúc với mặt cầu ( x - 2 ) 2 + ( y + 1 ) 2 + ( z - 3 ) 2 = 9 tại điểm M(6;-2;3) có phương trình là
Trong không gian Oxyz, cho mặt cầu (S):
x
-
1
2
+
y
+
2
2
+
z
-
5
2
9
. Phương trình nào dưới đây là phương trình mặt phẳng (P) tiếp xúc với mặt...
Đọc tiếp
Trong không gian Oxyz, cho mặt cầu (S):
x - 1 2 + y + 2 2 + z - 5 2 = 9 . Phương trình nào dưới đây là phương trình mặt phẳng (P) tiếp xúc với mặt cầu (S) tại điểm A(2;-4;3)?
A. x – 6y + 8z – 50 = 0
B. x – 2y – 2z – 4 = 0
C. x – 2y – 2z + 4 = 0
D. 3x – 6y + 8z – 54 = 0
Trong không gian Oxyz, cho mặt cầu (S) có phương trình là:
(
x
+
1
)
2
+
(
y
-
4
)
2
+
...
Đọc tiếp
Trong không gian Oxyz, cho mặt cầu (S) có phương trình là: ( x + 1 ) 2 + ( y - 4 ) 2 + ( z + 3 ) 2 = 36. Số mặt phẳng (P) chứa trục Ox và tiếp xúc với mặt cầu (S) là:
A. 0
B. 1
C. 2
D. Vô số
Đáp án A
Mặt cầu (S) có tâm I(-1;4;-3) và có bán kính R = 6. Gọi H là hình chiếu vuông góc của I trên trục Ox. Ta có H(-1;0;0) và IH=5.
Gọi K là hình chiếu vuông góc của I trên mặt phẳng (P). Ta có
d(I; (P)) = IK ≤ IH = 5 < R = 6
Do đó mặt phẳng (P) luôn cắt mặt cầu (S) theo một đường tròn. Vậy không tồn tại mặt phẳng (P) chứa Ox và tiếp xúc với (S)
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz viết phương trình mặt phẳng tiếp xúc với mặt cầu
x
-
1
2
+
y
2
+
z
+
2
2
6
đồng thời song song với hai đường thẳng
d
1
:...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz viết phương trình mặt phẳng tiếp xúc với mặt cầu x - 1 2 + y 2 + z + 2 2 = 6 đồng thời song song với hai đường thẳng d 1 : x - 2 3 = y - 1 - 1 = z - 1 ; d 2 : x 1 = y + 2 1 = z - 2 - 1 .
A. [ x - y + 2 z - 3 = 0 x - y + 2 z + 9 = 0
B. [ x + y + 2 z - 3 = 0 x + y + 2 z + 9 = 0
C. x + y + 2 z + 9 = 0
D. x - y + 2 z + 9 = 0
Ta có: (S) có tâm I 1 , 0 , - 2 và bán kính R = 6 .
d 1 có VTCP là: u 1 → 3 , - 1 , - 1
d 2 có VTCP là: u 2 → 1 , 1 , - 1
Ta có:
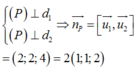
Khi đó ta có phương trình (P) có dạng:
x + y + 2 z + d = 0
Mặt phẳng (p) tiếp xúc với mặt cầu
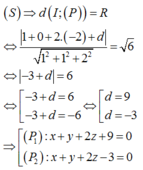
Chọn B.
Đúng 0
Bình luận (0)
Trong không gian Oxyz, phương trình mặt phẳng tiếp xúc với mặt cầu(S): (x-1)² + (y-2)² + (z-3)²81 tại điểm P(-5;-4;6) là: A. 7 x+8 y+670 B. 4 x+2 y-9 z+820 C. x-4 z+290 D. 2 x+2 y-z+240
Đọc tiếp
Trong không gian Oxyz, phương trình mặt phẳng tiếp xúc với mặt cầu(S): (x-1)² + (y-2)² + (z-3)²=81 tại điểm P(-5;-4;6) là:
A. 7 x+8 y+67=0
B. 4 x+2 y-9 z+82=0
C. x-4 z+29=0
D. 2 x+2 y-z+24=0
Đáp án D
Mặt cầu (S) có tâm I(1;2;3).
Gọi (α) là mặt phẳng cần tìm. Do (α) tiếp xúc với (S) tại P nên mặt phẳng (α) đi qua P và có véc-tơ pháp tuyến 
Phương trình mặt phẳng (α) là:
-6(x+5)-6(y+4)+3(z-6) = 0 <=> 2x + 2y - z + 24 = 0.
Đúng 0
Bình luận (0)
Trong không gian Oxyz, cho điểm M (1;1;-2) và mặt phẳng (α) : x - y - 2z = 2. Viết phương trình mặt cầu (S) có tâm M tiếp xúc với mặt phẳng (α)
Lời giải:
Bán kính mặt cầu là:
\(R=d(M, (a))=\frac{|1-1-2(-2)-2|}{\sqrt{1^2+1^2+2^2}}=\frac{\sqrt{6}}{3}\)
PT mặt cầu $(S)$ là:
$(x-1)^2+(y-1)^2+(z+2)^2=\frac{2}{3}$
Đúng 0
Bình luận (0)
Trong không gian với hệ trục Oxyz cho điểm A(2;1;3) và đường thẳng có phương trình
(
d
)
:
x
-
1
2
y
-
2
-
1
z
1
.
Mặt phẳng (P) chứa A và d. Viết phương trình mặt cầu tâm O tiếp xúc với mặt phẳng (...
Đọc tiếp
Trong không gian với hệ trục Oxyz cho điểm A(2;1;3) và đường thẳng có phương trình ( d ) : x - 1 2 = y - 2 - 1 = z 1 . Mặt phẳng (P) chứa A và d. Viết phương trình mặt cầu tâm O tiếp xúc với mặt phẳng (P).
A. x 2 + y 2 + z 2 = 12 5
B. x 2 + y 2 + z 2 = 3
C. x 2 + y 2 + z 2 = 6
D. x 2 + y 2 + z 2 = 24 5
Đáp án D.
( d ) : x - 1 2 = y - 2 - 1 = z 1 đi qua B(1;2;0) có vecto chỉ phương n d → = 2 ; - 1 ; 1
Với B A → = 1 ; - 1 ; 3 , vecto pháp tuyến của (P) là: B A → , u d → = 2 ; 5 ; 1
⇒ P : 2 x - 2 + 5 y - 1 + z - 3 = 0 ⇔ 2 x + 5 y + z - 12 = 0
Bán kính của mặt cầu cần tìm là d O , P = 2 30 5 .
Đúng 0
Bình luận (0)