Cho ( C ) : y = x 2 + 5 x - 1 . Gọi là hoành độ các điểm cực tiểu, cực đại của (C). Khi đó
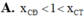
![]()
![]()
![]()
cho x + y+z=0. cmr 2(x^5+y^5+z^5)=5xyz(x^2+y^2+z^2)
cho a+b+c=0;a^2+b^2+c^2=0;a^3+b^3+c^3=0. tính a+b^2+c^3
Tìm số nguyên x, y sao cho:
a) x. y = -5
b) x. y = -5 và x > y
c) (x + 1).(y - 2) = -5
Viết số -5 thành tích của hai số nguyên theo tất cả các cách, ta có: -5 = l.(-5)=(-5).l = (-l).5 = 5.(-l).
Từ đó ta tìm được x,y thỏa mãn điều kiện đề bài.
a) Các cặp số (x ; y) tìm được là: (1;-5),(-5; 1), (-1;5),(5; -1)
b) Dựa vào câu a và kết hợp điều kiện x > y, ta tìm được các cặp số (x;y) sau: (5;-l),(l;-5).
c) Làm tương tự câu a, ta tìm được x + 1 và y - 2. Từ đó suy ra (x;y) là (0;-3), (-6; 3), (-2; 7), (4; 1).
a) cho x+y=a ; x.y =b . Tính
A=x^2+y^2 ; B=x^3+y^3 ; C=x^5+y^5
b) cho x+y=1 . Tính M= 2.(x^3+y^3 ) - 3. ( x^2+y^2 )
a)
A=\(x^2+y^2=\left(x^2+2xy+y^2\right)-2xy=\left(x+y\right)^2-2xy=a^2-2b\)
\(B=x^3+y^3=\left(x^3+3x^2y+3xy^2+y^3\right)-3x^2y-3xy^2=\left(x+y\right)^3-3xy\left(x+y\right)=a^3-3ab\)
\(C=x^5+y^5=\left(x^5+y^5+5x^4y+10x^3y^2+10x^2y^3+5xy^4\right)-5x^4y-10x^3y^2-10x^2y^3-5xy^4\)
\(=\left(x+y\right)^5-5xy\left(x^3+2xy^2+2x^2y+y^3\right)=\left(x+y\right)^5-5xy\left(x^3+3xy^2+3x^2y+y^3-xy^2-x^2y\right)\)
\(=\left(x+y\right)^5-5xy\left(\left(x+y\right)^3-xy\left(x+y\right)\right)=a^5-5b\left(a^3-ab\right)\)
Tìm các số nguyên x, y sao cho:
a) x . y = - 5;
b) x . y = - 5 và x > y;
c) ( x + l) ( y - 2) = - 5.
Viết số -5 thành tích của hai số nguyên theo tất cả các cách, ta có:
-5 = l.(-5)=(-5).l = (-l).5 = 5.(-l). Từ đó ta tìm được x,y thỏa mãn điều kiện đề bài.
a) Các cặp số (x ; y) tìm được là: (1;-5),(-5; 1), (-1;5),(5; -1)
b) Dựa vào câu a và kết hợp điều kiện x > y, ta tìm được các cặp số (x;y) sau: (5;-l),(l;-5).
c) Làm tương tự câu a, ta tìm được x + 1 và y - 2. Từ đó suy ra (x;y) là (0;-3), (-6; 3), (-2; 7), (4; 1).
Tìm các số nguyên x, y sao cho:
a) x . y = - 5;
b) x . y = - 5 và x > y;
c) ( x + l) ( y - 2) = - 5
Viết số -5 thành tích của hai số nguyên theo tất cả các cách, ta có: -5 = l.(-5)=(-5).l = (-l).5 = 5.(-l). Từ đó ta tìm được x,y thỏa mãn điều kiện đề bài. a) Các cặp số (x ; y) tìm được là: (1;-5),(-5; 1), (-1;5),(5; -1) b) Dựa vào câu a và kết hợp điều kiện x > y, ta tìm được các cặp số (x;y) sau: (5;-l),(l;-5). c) Làm tương tự câu a, ta tìm được x + 1 và y - 2. Từ đó suy ra (x;y) là (0;-3), (-6; 3), (-2; 7), (4; 1)
Cho x, y, z là các số thực dương thoả mãn xyz=1 . Chứng minh rằng:
\(\dfrac{x^5-x^2}{x^5+y^2+z^2}+\dfrac{y^5-y^2}{y^5+x^2+z^2}+\dfrac{z^5-z^2}{z^5+x^2+y^2}\ge0\)
\(\Sigma\left(\dfrac{x^5-x^2}{x^5+y^2+z^2}\right)\ge0\)
\(\Leftrightarrow\Sigma\left(1-\dfrac{x^5-x^2}{x^5+y^2+z^2}\right)\le3\)
\(\Leftrightarrow\Sigma\left(\dfrac{x^2+y^2+z^2}{x^5+y^2+z^2}\right)\le3\)
\(\Leftrightarrow\dfrac{1}{x^5+y^2+z^2}+\dfrac{1}{y^5+x^2+z^2}+\dfrac{1}{z^5+x^2+y^2}\le\dfrac{3}{x^2+y^2+z^2}\)
Áp dụng bất đẳng thức Bunyakovsky
\(\Rightarrow\left(x^5+y^2+z^2\right)\left(\dfrac{1}{x}+y^2+z^2\right)\ge\left(x^2+y^2+z^2\right)^2\)
\(\Rightarrow\dfrac{1}{x^5+y^2+z^2}\le\dfrac{\dfrac{1}{x}+y^2+z^2}{\left(x^2+y^2+z^2\right)^2}\)
Thiết lập tương tự và thu lại ta có
\(\Rightarrow\dfrac{1}{x^5+y^2+z^2}+\dfrac{1}{y^5+x^2+z^2}+\dfrac{1}{z^5+x^2+y^2}\le\dfrac{\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}+2\left(x^2+y^2+z^2\right)}{\left(x^2+y^2+z^2\right)^2}\)
Chứng minh rằng \(\dfrac{\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}+2\left(x^2+y^2+z^2\right)}{\left(x^2+y^2+z^2\right)^2}\le\dfrac{3}{x^2+y^2+z^2}\)
\(\Leftrightarrow\dfrac{\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}+2\left(x^2+y^2+z^2\right)}{\left(x^2+y^2+z^2\right)^2}\le\dfrac{x^2+y^2+z^2+2\left(x^2+y^2+z^2\right)}{\left(x^2+y^2+z^2\right)^2}\)
\(\Leftrightarrow\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}\le x^2+y^2+z^2\) ( vì \(xyz=1\) )
\(\Leftrightarrow xy+yz+xz\le x^2+y^2+z^2\) ( luôn đúng theo hệ quả của bất đẳng thức Cauchy )
\(\Rightarrow\) đpcm
Dấu " = " xảy ra khi \(x=y=z=1\)
Cho A = { 2; 5 }; B = { 5; x }; C = { x; y; 5 }. tìm các cặp số ( x; y ) để A = B = C
A=B
=>x=2
=>A={2;5}; B={5;2}; C={2;y;5}
B=C
=>y phải trùng với 2 hoặc 5
=>\(y\in\left\{2;5\right\}\)
1 .Cho x+y=a và xy=b , tính giá trị của biểu thức :
a. x^2+y^2
b. x^3+y^3
c. x^4+y^4
d. x^5+y^5
2 . a.Cho x+y=1 tính GTBT x^3+y^3+xy
b. cho x-y=1 tính GTBT x^3-y^3-xy
c. cho x+y=a , x^2+y^2=b tính x^3+y^3
(x+y)^2 =a^2
x^2 +2xy +y^2 =a^2
x^2+y^2 =a^2-2xy =a^2 -2b
x^3 +y^3 = (x+y)(x^2 -xy +y^2)
=a(a^2-2b-b)
=a(a^2-3b)
=a^3- 3ab
(x^2 +y^2)^2=(a^2-2b)^2 ( cái này tính cho x^4 + y^4)
tương tự như câu đầu tiên
x^5+ y^5 (cái đó mình không biết)
\(1.\)
\(a)\)
\(x^2+y^2\)
\(=\left(x+y\right)^2-2xy\)
\(=a^2-2b\)
\(b)\)
\(x^3+y^3\)
\(=\left(x+y\right)\left(x^2-xy+y^2\right)\)
\(=a[\left(x+y\right)^2-3xy]\)
\(=a\left(a^2-3b\right)\)
\(=a^3-3ab\)
\(c)\)
\(x^4+y^4\)
\(=\left(x^2+y^2\right)^2-2x^2y^2\)
\(=\left(a^2-2b\right)^2-2b^2\)
\(=a^4-4a^2b+2b^2\)
\(d)\)
\(x^5+y^5\)
\(=\left(x^2+y^2\right)\left(x^3+y^3\right)-x^2y^2\left(x+y\right)\)
\(=[\left(x+y\right)^2-2xy][\left(x+y\right)^3-3xy\left(x+y]\right)-ab^2\)
\(=\left(a^2-2b\right)\left(a^3-3ab\right)-ab^2\)
\(=a^5-3a^3b-2a^3b+6ab^2-ab^2\)
\(=a^5-5a^3b+5ab^2\)
1, x/y = 9/7;y/z = 7/9 va x-y+z=-15
b.6/11 x= 9/2 y=18/5z va -x+y+z=3
c,x/5=y/7=z/3 va x^2+y^2-z^2=585io
d,cho x/y/z =5/4/3 tinh P=x+2y-3z/x-2y+3z
e,cho 2a+b+c/a = a+2b+c/b = a+b+2c/c tinh S=a+b/c + b+c/a + c+a/b
B1 cho x+y=30 và x*y=100. Tính. a, x^2+y^2. b, x^3+y^3 c, x^4+y^4. d, x^5+y^5