Cho hàm số y = x5 - x -1 có đồ thị (C). Chọn khẳng định đúng
Những câu hỏi liên quan
Biết hàm số yf(x) có đồ thị đối xứng với đồ thị hàm số
y
3
x
qua đường thẳng x-1. Chọn khẳng định đúng trong các khẳng định sau? A.
f
(
x
)
1
3
.
3
x
B.
f
(
x
)...
Đọc tiếp
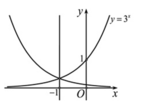
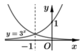
Biết hàm số y=f(x) có đồ thị đối xứng với đồ thị hàm số y = 3 x qua đường thẳng x=-1. Chọn khẳng định đúng trong các khẳng định sau?
A. f ( x ) = 1 3 . 3 x
B. f ( x ) = 1 9 . 3 x
C. f ( x ) = 1 3 x - 1 2
D. f ( x ) = - 2 + 1 3 x
Biết hàm số
y
f
x
có đồ thị đối xứng với đồ thị hàm số
y
3
x
qua đường thẳng
x
-
1
. Chọn khẳng định đúng trong các khẳng định sau A.
f
x
1
3
.
3
x
B.
f
x
1...
Đọc tiếp
Biết hàm số y = f x có đồ thị đối xứng với đồ thị hàm số y = 3 x qua đường thẳng x = - 1 . Chọn khẳng định đúng trong các khẳng định sau
A. f x = 1 3 . 3 x
B. f x = 1 9 . 3 x
C. f x = 1 3 x - 1 2
D. f x = - 2 + 1 3 x
Gọi M(x;y) và M'(x';y') là hai điểm đối xứng nhau qua đường thẳng x = -1 nên
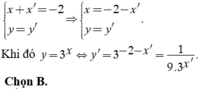
Trắc nghiệm: Chọn
A'(-2;1) chỉ có đáp án B thỏa.
Đúng 0
Bình luận (0)
Cho hàm số y f (x) có đồ thị (C) như hình vẽ. Chọn khẳng định đúng về hàm số f (x) A. Hàm số
f
(
x
)
có điểm cực đại là
0
;
1
. B. Hàm số
f
(
x
)...
Đọc tiếp
Cho hàm số y = f (x) có đồ thị (C) như hình vẽ. Chọn khẳng định đúng về hàm số f (x)
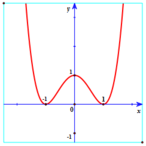
A. Hàm số f ( x ) có điểm cực đại là 0 ; 1 .
B. Hàm số f ( x ) có điểm cực tiểu là 0 ; 1 .
C. Hàm số f ( x ) có ba điểm cực trị.
D. Hàm số f ( x ) có ba giá trị cực trị.
Chọn C.
Từ đồ thị suy ra hàm số đạt cực đại tại x = 0 và đạt cực tiểu tại x = ± 1 nên loại A, B, D
Đúng 0
Bình luận (0)
Biết hàm y f(x) có đồ thị đối xứng với đồ thị hàm
y
3
x
qua đường thẳng x -1. Chọn khẳng định đúng trong các khẳng định sau A.
f
x
1
3.3
x
B.
f
x
1
9
.3...
Đọc tiếp
Biết hàm y = f(x) có đồ thị đối xứng với đồ thị hàm y = 3 x qua đường thẳng x= -1. Chọn khẳng định đúng trong các khẳng định sau
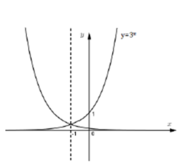
A. f x = 1 3.3 x
B. f x = 1 9 .3 x
C. f x = 1 3 x − 1 2
D. f x = − 2 + 1 3 x
Đáp án B
Phương pháp:
Lấy điểm A(0;1) thuộc đồ thị
Đúng 0
Bình luận (0)
Cho hàm số
y
x
4
+
b
x
2
+
c
có đồ thị (C). Chọn khẳng định đúng nhất: A. Đồ thị (C) có ít nhất một điểm cực đại. B. Đồ thị (C) có đúng một điểm cực tiểu. C. Đồ thị (C) có ít nhất một điểm cực tiểu. D. Đồ thị (C) có đúng một điểm cực đại.
Đọc tiếp
Cho hàm số y = x 4 + b x 2 + c có đồ thị (C). Chọn khẳng định đúng nhất:
A. Đồ thị (C) có ít nhất một điểm cực đại.
B. Đồ thị (C) có đúng một điểm cực tiểu.
C. Đồ thị (C) có ít nhất một điểm cực tiểu.
D. Đồ thị (C) có đúng một điểm cực đại.
Chọn C.
Do a = 1 > 0 nên (C) có 2 trường hợp là có 1 điểm cực tiểu hay có 2 điểm cực tiểu và một điểm cực đại.
Đúng 0
Bình luận (0)
Cho hàm số yf(x) thỏa mãn f(-x)f(x). Gọi đồ thị hàm số là (C). Chọn khẳng định đúng
Đọc tiếp
Cho hàm số y=f(x) thỏa mãn f(-x)=f(x). Gọi đồ thị hàm số là (C). Chọn khẳng định đúng
Cho hàm số yf(x) có đồ thị như hình dưới đây. Chọn khẳng định đúng A. Hàm số liên tục trên (-
∞
;4). B. Hàm số liên tục trên (1;4). C. Hàm số liên tục trên R. D. Hàm số liên tục trên (1;+
∞
).
Đọc tiếp
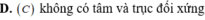
Cho hàm số y=f(x) có đồ thị như hình dưới đây. Chọn khẳng định đúng
A. Hàm số liên tục trên (- ∞ ;4).
B. Hàm số liên tục trên (1;4).
C. Hàm số liên tục trên R.
D. Hàm số liên tục trên (1;+ ∞ ).
Cho hàm số y f(x) có đồ thị như hình dưới đây. Chọn khẳng định đúng. A. Hàm số liên tục trên (-
∞
;4). B. Hàm số liên tục trên (1;4). C. Hàm số liên tục trên R D. Hàm số liên tục trên (1;+
∞
).
Đọc tiếp
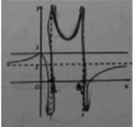
Cho hàm số y = f(x) có đồ thị như hình dưới đây. Chọn khẳng định đúng.
A. Hàm số liên tục trên (- ∞ ;4).
B. Hàm số liên tục trên (1;4).
C. Hàm số liên tục trên R
D. Hàm số liên tục trên (1;+ ∞ ).
Chọn B.
Phương pháp:
Dựa vào đồ thị hàm số để nhận xét và chọn đáp án đúng.
Cách giải:
Hàm số liên tục trên (1;4).
Đúng 0
Bình luận (0)
Cho hàm số f(x) liên tục trên
ℝ
hàm số y f (x) có đồ thị như hình vẽ. Xét hàm số
h
x
2
f
3
x
+
1
-
9
x
2
-
6
x
+
4
. Hãy chọn khẳng định đúng: A. Hàm số h(x) nghịch biến trên
ℝ
B. Hàm số h(x) nghịch biến trên ...
Đọc tiếp
Cho hàm số f(x) liên tục trên ℝ hàm số y = f '(x) có đồ thị như hình vẽ. Xét hàm số h x = 2 f 3 x + 1 - 9 x 2 - 6 x + 4 . Hãy chọn khẳng định đúng:
A. Hàm số h(x) nghịch biến trên ℝ
B. Hàm số h(x) nghịch biến trên - 1 ; 1 3
C. Hàm số h(x) đồng biến trên - 1 ; 1 3
D. Hàm số h(x) đồng biến trên ℝ
