Trong không gian Oxy, cho đường thẳng d: x - 1 - 1 = y + 4 2 = z - 3 3 Véctơ nào sau đây không phải là véctơ chỉ phương của đường thẳng d?
![]()
![]()
![]()
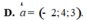
Trong không gian Oxyz, cho đường thẳng d: x = 1 + t, y = 2 -2t, z = -3. Viết phương trình tham số của đường thẳng Δ nằm trong mặt phẳng (Oxy), song song với d sao cho khoảng cách giữa hai đường thẳng d và Δ đạt giá trị nhỏ nhất
A. d: x = 1 + t, y = 2 -2t, z = 0
B. d: x = 1 + t, y = -2t, z = -3
C. d: x = t, y = 2 - 2t, z = -3
D. d: x = 1, y = 2, z = -3 + t
Đáp án A
*Gọi (Q) là mặt phẳng chứa d và vuông góc với mặt phẳng (Oxy). Để khoảng cách giữa hai đường thẳng d và ∆ nhỏ nhất thì ∆ chính là giao tuyến của hai mặt phẳng (Oxy) và mp (Q).
* Mặt phẳng (Oxy) có phương trình là z = 0 có VTPT n Oxy → = (0; 0; 1).
Đường thẳng d đi qua A(1;2; -3) và có VTCP u d → = (1; -2; 0)
Suy ra, VTPT của (Q) là n Q → = [ u d → ; n Oxy → ] = (2; 1; 0)
Phương trình mặt phẳng (Q) là: 2(x - 1) + 1(y - 2) + 0(z + 3) = 0
Hay 2x + y -4 =0
* Đường thẳng ∆ cần tìm là giao tuyến của hai mặt phẳng (Oxy) và (Q). Tập hợp các điểm thuộc ∆ là nghiệm hệ phương trình: 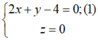
* Đặt x = 1 + t thay vào (1) ta được: y = 4 - 2x = 4 - 2(1 + t) = 2 - 2t
Suy ra, phương trình tham số của đường thẳng ∆ là: 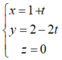
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d có phương trình x = 1 + 2 t y = t z = 2 - t . Gọi d’là hình chiếu vuông góc của đường thẳng d trên mặt phẳng (Oxy). Đường thẳng d’ có một véc tơ chỉ phương là
A. u 1 → = ( 2 ; 0 ; 1 )
B. u 1 → = ( 1 ; 1 ; 0 )
C. u 1 → = ( - 2 ; 1 ; 0 )
D. u 1 → = ( 2 ; 1 ; 0 )
Đáp án D
Gọi M(1+2t;2t;2-t) là giao điểm của d và (Oxy): z =0
![]()
Gọi N(1;0;2) là điểm thuộc d. Hình chiếu của N lên (Oxy) là I(1;0;0)
![]()
là một véc tơ chỉ phương của d’
Trong không gian với hệ trục tọa độ Oxyz, cho đường thẳng ∆ : x - 1 2 = y - 1 1 = z - 1 - 1 và mặt phẳng P : x+y+z-3=0. Gọi d là đường thẳng nằm trong (P), đi qua giao điểm của Δ và (P), đồng thời vuông góc với Δ. Giao điểm của đường thẳng d với mặt phẳng tọa độ (Oxy) là
A. M(2;2;0)
B. M(-3;2;0)
C. M(-1;4;0)
D. M(-3;4;0)
Trong không gian Oxyz, cho mặt phẳng ( α ) : 2 x + y - 2 z - 2 = 0 , đường thẳng d : x + 1 1 = y + 2 2 = z + 3 2 và điểm A(1/2; 1; 1). Gọi ∆ là đường thẳng nằm trong mặt phẳng ( α ) , song song với d đồng thời cách d một khoảng bằng 3. Đường thẳng ∆ cắt mặt phẳng Oxy tại điểm B. Độ dài đoạn thẳng AB bằng
A. 7 / 3
B. 7 / 2
C. 21 / 2
D. 3 / 2
Trong không gian Oxyz, đường thẳng d : x - 3 1 = y + 2 - 1 = z - 4 2 cắt mặt phẳng (Oxy) tại điểm có tọa độ là:
A. M(-3;2;0)
B. M(3;-2;0)
C. M(-1;0;0)
D. M(1;0;0)
Đáp án D
Phương pháp:
+) Gọi M là giao điểm của đường thẳng d và mặt phẳng (Oxy). Khi đó tọa độ điểm M thỏa mãn phương trình đường thẳng d và mặt phẳng (Oxy).
+) Phương trình mặt phẳng (Oxy): z=0
Cách giải:
Gọi M x 0 ; y 0 ; z 0 là giao điểm của đường thẳng d và mặt phẳng (Oxy): z 0 = 0
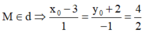
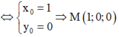
Trong không gian với hệ tọa độ Oxy, cho hai đường thẳng d 1 : x = 2 + t y = 1 − t z = 2 t và d 2 : x = 2 − 2 t y = 3 z = t . Khoảng cách từ điểm M − 2 ; 4 ; − 1 đến mặt phẳng cách đều hai đường thẳng d 1 và d 2 là:
A. 15 15
B. 2 15 15
C. 30 15
D. 2 30 15
Đáp án D
Nhận thấy d 1 ⊥ d 2 . Gọi α là mặt phẳng cách đều d 1 và d 2 nên cả hai đường thẳng đều song song với mặt phẳng α . Khi đó, vector pháp tuyến a → của mặt phẳng α cùng phương với vector u 1 → , u 2 → (với u 1 → , u 2 → lần lượt là các vec tơ chỉ phương của hai đường thẳng d 1 , d 2 ).
+ Chọn a → = 1 ; 5 ; 2 , suy ra phương trình mặt phẳng α có dạng
α : x + 5 y + 2 z + d = 0
Chọn A 2 ; 1 ; 0 và B 2 ; 3 ; 0 lần lượt thuộc đường thẳng d 1 và d 2 , ta có
d A ; α = d B ; β ⇒ d = − 12 ⇒ α : x + 5 y + 2 z − 12 = 0
+ Khoảng cách từ điểm M − 2 ; 4 ; − 1 đến mặt phẳng α : d M ; α = 2 30 15
Trong không gian với hệ tọa độ Oxy, cho đường thẳng ∆ : x - 1 2 = y 1 = z + 2 - 1 và hai điểm A(0;-1;3), B(1;-2;1). Tìm tọa độ điểm M thuộc đường thẳng Δ sao cho M A 2 + 2 M B 2 đạt giá trị nhỏ nhất.
![]()
![]()
![]()
![]()
Trong không gian với hệ tọa độ Oxy, cho đường thẳng △ : x - 1 2 = y 1 = z + 2 - 1 và hai điểm A(0;-1;3), B(1;-2;1). Tìm tọa độ điểm M thuộc đường thẳng Δ sao cho M A 2 + 2 M B 2 đạt giá trị nhỏ nhất
A. M(5;2;-4)
B. M(-1;-1;-1)
C. M(1;0;-2)
D. M(3;1;-3)
Trong không gian Oxyz, cho mặt phẳng ( α ) : 2 x + y - 2 z - 2 = 0 đường thẳng d : x + 1 1 = y + 2 2 = z + 3 2 và điểm A 1 2 ; 1 ; 1 . Gọi ∆ là đường thẳng nằm trong mặt phẳng ( α ) , song song với d đồng thời cách d một khoảng bằng 3. Đường thẳng ∆ cắt mặt phẳng (Oxy) tại điểm B. Độ dài đoạn thẳng AB bằng
A. 7 3
B. 7 2
C. 21 2
D. 3 2
Đáp án B
Phương pháp:
![]()
![]()
![]()
thay tọa độ điểm B vào phương trình ( α ) => 1 phương trình 2 ẩn a, b.
![]()
Sử dụng công thức tính khoảng cách
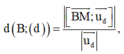
lập được 1 phương trình 2 ẩn chứa a, b.
+) Giải hệ phương trình tìm a,b => Toạ độ điểm B => Độ dài AB.
Dế thấy
![]()
Ta có
![]()
![]()
![]()
Lại có
![]()
Đường thẳng d đi qua M(0;0;-1), có u → = ( 1 ; 2 ; 2 )
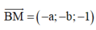
![]()
Do đó
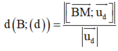
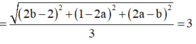
![]()
![]()
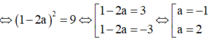
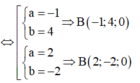
Vậy AB = 7 2