Cho hình lăng trụ ABCD.A'B'C'D' có hình chiếu A' lên (ABCD) là trung điểm AB, ABCD là hình thoi cạnh 2a, góc A B C ^ = 60 0 , BB' tạo với đáy một góc 30 0 . Tính thể tích hình lăng trụ ABCD.A'B'C'D'.
A. a 3 3
B. 2 a 3 3
C. 2 a 3
D. a 3
Cho hình lăng trụ A B C D . A ' B ' C ' D ' có đáy ABCD là hình thoi cạnh a, tâm O và A B C = 120 ° . Các cạnh AA', A'B, A' D cùng tạo với đáy một góc 60 ° .Tính theo a thể tích V của khối lăng trụ đã cho.
A. a 3 3
B. a 3 3 6
C. a 3 3 2
D. 3 a 3 2
Đáp án C
Ta có: A B C ^ = 120 ∘ ⇒ B A D ^ = 60 ∘ suy ra tam giác ABD là tam giác đều cạnh a. Khi đó A’.ABD là chóp đều cạnh đáy bằng a. Như vậy hình chiếu vuông góc của A’ lên mặt đáy trùng với trọng tâm tam giác ABD.
Ta có: A ' H = HA tan 60 ∘ = a 3 3 . 3 = a
⇒ V A ' A B D = 1 3 A ' H . S A B C = a 3 3 12
Do đó V A B C D . A ' B ' C ' D ' = 3 V A ' . A B C D = 6 V A ' A B D = a 3 3 2 .
Cho hình lăng trụ ABCD.A'B'C'D' có đáy ABCD là hình thoi cạnh a, tâm O và ABC= 120 o . Các cạnh AA', A'B, A' D cùng tạo với đáy một góc 60 o .Tính theo a thể tích V của khối lăng trụ đã cho.
A. a 3 3
B. a 3 3 6
C. a 3 3 2
D. 3 a 2 2
Cho hình lăng trụ ABCD.A'B'C'D' có hình chiếu A' lên mp(ABCD) là trung điểm AB, ABCD là hình thoi cạnh 2a, góc A B C ^ = 60 ° , BB' tạo với đáy một góc 30 ° . Tính thể tích hình lăng trụ ABCD.A'B'C'D'.
A. a 3 3
B. 2 a 3 3
C. 2 a 3
D. a 3
Đáp án là A
+ Tính 
+ Tính A'H:
Ta có: 
( Vì AH là hình chiếu của AA' trên mp(ABCD)).
Suy ra: 
Vậy: 
Cho hình lăng trụ ABCD.A'B'C'D' có hình chiếu A' lên mp(ABCD) là trung điểm AB, ABCD là hình thoi cạnh 2a, góc A B C ^ = 60 O ,BB' tạo với đáy một góc 30 o . Tính thể tích hình lăng trụ ABCD.A'B'C'D'
A. a 3 3
B. 2 a 3 3
C. 2 a 3
D. a 3
Đáp án là C
Gọi H là hình chiếu của A’ trên (ABCD). Dễ thấy góc
Dễ dàng tính được diện tích đáy
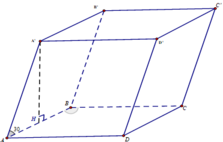
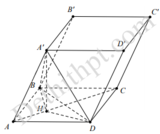
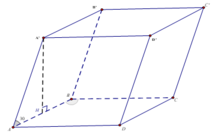
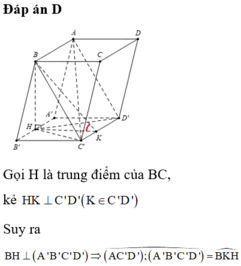
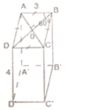
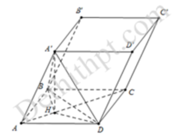
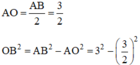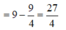Cho lăng trụ ABCD.A'B'C'D' có đáy ABCD là hình thoi, AC=2a, BAD= 120 o Hình chiếu vuông góc của điểm B trên mặt phẳng (A'B'C'D') là trung điểm cạnh A' B' góc giữa mặt phẳng (AC'D') và mặt đáy lăng trụ bằng 60 o . Tính thể tích V của khối lăng trụ ABCD.A'B'C'D'?
Cho lăng trụ đứng A B C D . A ' B ' C ' D ' có đáy ABCD là hình thoi có độ dài cạnh 3cm, góc ∠ A B C = 60 o và chiều cao AA’ của hình lăng trụ bằng 4cm. Tính:
a) Diện tích xung quanh của hình lăng trụ.
b) Thể tích của hình lăng trụ đó.
a) Sxq = 2.P.H (p: chu vi đáy; h: chiều cao)
= 3(3 + 3).4 = 48(cm2)
b) Gọi O là giao điểm của AC và BD. Vì tứ giác ABCD là hình thoi nên AC ⊥ BD tại O và có ∠ABC = 60o => ∠ABO = 30o
ΔABO là nửa tam giác đều nên
cho lăng trụ đứng ABCD.A'B'C'D' có đáy ABCD là hình thoi cạnh bằng a, góc ABC =60 độ, AA'= 3a. tính thể tích khối lăng trụ đó
Gọi O là tâm hình thoi ABCD.
Do ABCD là hình thoi mà \(\widehat{ABC}=60^o\)
⇒ Tam giác ABC đều.
⇒ \(BO=\dfrac{AB\sqrt{3}}{2}=\dfrac{a\sqrt{3}}{2}\)
⇒ \(BD=2BO=a\sqrt{3}\)
\(V_{ABCD.A'B'C'D'}=AA'\cdot S_{ABCD}=3a\cdot\dfrac{1}{2}\cdot a\sqrt{3}\cdot a=\dfrac{3a\sqrt{3}}{2}\)
Cho hình lăng trụ A B C D . A ' B ' C ' D ' có đáy ABCD là hình thoi cạnh a, tâm O và A B C ^ = 120 ° . Các cạnh AA, A'B, A'D cùng tạo với mặt đáy một góc bằng 60 ° . Tính theo a thể tích V của khối lăng trụ đã cho
A. V = a 3 3
B. V = a 3 3 6
C. V = a 3 3 2
D. V = 3 a 3 2
Đáp án C
Ta có: A B C ^ = 120 ∘ ⇒ B A D ^ = 60 ∘ suy ra tam giác ABD là tam giác đều cạnh a. Khi đó A’.ABD là chóp đều cạnh đáy bằng a. Như vậy hình chiếu vuông góc của A’ lên mặt đáy trùng với trọng tâm tam giác ABD.
