Cho tứ diện ABCD có các cạnh A D = B C = 3 , A C = B D = 4 ; A B = C D = 2 3 . Thể tích tứ diện ABCD bằng:
A. 2740 12
B. 2047 12
C. 2074 12
D. 2470 12
Cho S là diện tích của tứ giác ABCD có độ dài các cạnh là a, b, c, d. Chứng minh S ≤ (a^2 + b^2 + c^2 + d^2)/4
Cho tứ giác ABCD có số đo các cạnh là a,b,c,d (a,b,c,d là các số nguyên dương). Biết a,b,c,d đều là các ước của a+b+c+d. CMR: tứ giác ABCD có ít nhất hai cạnh bằng nhau.
Trong không gian với hệ trục tọa độ Oxyz ,cho tứ diện ABCD có tọa độ các điểm A(1;1;1), B(2;0;2), C(-1;-1;0), D(0;3;4). Trên các cạnh AB, AC, AD lần lượt lấy các điểm B',C', D' sao cho A B A B ' + A C A C ' + A D A D ' = 4 và tứ diện AB'C'D' có thể tích nhỏ nhất. Phương trình mặt phẳng (B'C'D') là
A. 16x-40y-44z+39=0
B. 16x-40y-44z-39=0
C. 16x+40y+44z-39=0
D. 16x+40y-44z+39=0
Chọn D
Trên cạnh AB, AC , AD của tứ diện ABCD lần lượt có các điểm B', C', D'. Áp dụng công thức tỷ số thể tích ta có
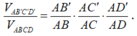
Từ giả thiết
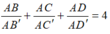
áp dụng bất đẳng thức AM- GM ta có
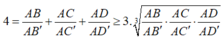
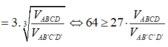
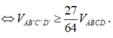
Do thể tích ABCD cố định nên thể tích AB'C'D' nhỏ nhất
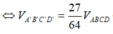
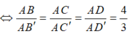
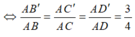
=> (B'C'D') song song với (BCD) và đi qua điểm B'
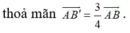
![]()
![]()
suy ra vectơ pháp tuyến của mặt phẳng (B'C'D') là:
![]()
![]()
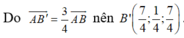
Vậy phương trình (B'C'D') là:
![]()
Trong không gian với hệ tọa độ Oxyz, cho tứ diện ABCD có tọa độ các điểm A(1;1;1), B(2;0;2), C(-1;-1;0), D(0;3;4). Trên các cạnh AB, AC, ADlần lượt lấy các điểm B’,C’,D’ sao cho A B A B ' + A C A C ' + A D A D ' = 4 và tứ diện AB’C’D’ có thể tích nhỏ nhất. Phương trình mặt phẳng (B’C’D’) là
A. 16x-40y-44z-39=0.
B. 16x-40y-44z+39=0.
C. 16x+40y+44z-39=0.
D. 16x+40y-44z+39=0.
Trong không gian với hệ trục tọa độ Oxyz, cho tứ diện ABCD có điểm A(1;1;1) , B(2;0;2), C(-1; -1; 0), D(0;3;4) Trên các cạnh AB, AC, AD lần lượt lấy các điểm B', C', D' thỏa: A B A B ' + A C A C ' + A D A D ' = 4 Viết phương trình mặt phẳng (B'C'D') biết tứ diện AB'C'D' có thể tích nhỏ nhất?
A. 16x+40y+44z-39=0
B. 16x+40y-44z+39=0
C. 16x-40y-44z+39=0
D. 16x-40y-44z-39=0
Chọn C
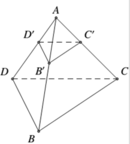
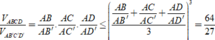
![]()
Dấu = xảy ra khi:![]()
Suy ra 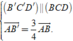
Ta có 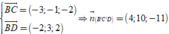
Mặt khác
![]()
Vậy phương trình mặt phẳng (B' C' D') là ![]()
Trong không gian Oxyz, cho tứ diện ABCD có A (1;1;1), B (2;0;2), C ( -1;-1;0) và D ( 0;3;4). Trên các cạnh AB , AC, AD lần lượt lấy các điểm B', C', D' sao cho thể tích của khối tứ diện AB'C'D' nhỏ nhất và A B A B ' + A C A C ' + A D A D ' = 4 . Tìm phương trình của mặt phẳng (B’C’D’)
A. 16 x + 40 y - 44 z + 39 = 0
B. 16 x - 40 y - 44 z + 39 = 0
C. 16 x + 40 y + 44 z + 39 = 0
D. 16 x + 40 y - 44 z - 39 = 0
Cho tứ giác ABCD có độ dài các cạnh là a, b, c, d đều là các số tự nhiên. Biết tổng S = a + b + c + d chia hết cho a, cho b, cho c, cho d. Chứng minh rằng tồn tại hai cạnh của tứ giác bằng nhau.
Giả sử tứ giác ABCD có AD = a, AB = b, BC = c, CD = d không có hai cạnh nào bằng nhau. Ta có thể giả sử a < b < c < d.
Ta có a + b + c > BD + c > d.
Do đó a + b + c + d > 2d hay S > 2d (*)
Ta có: S\(⋮\)a => S = m.a (m\(\in\)N) (1)
S\(⋮\)b => S = n.b (n\(\in\)N) (2)
S\(⋮\)c => S = p.d (p\(\in\)N) (3)
S\(⋮\)d => S = q.d (q\(\in\)N) (4) . Từ (4) và (*) suy ra q.d > 2d => q > 2
Vì a < b < c < d (theo giả sử) nên từ (1), (2), (3) và (4) suy ra m > n > p > q > 2
Do đó q\(\ge\)3; p\(\ge\)4; n\(\ge\)5; m\(\ge\)6
Từ (1), (2), (3), (4) suy ra 1/m = a/S; 1/n = b/S; 1/p = c/S; 1/q = d/S
Ta có: \(\frac{1}{6}+\frac{1}{5}+\frac{1}{4}+\frac{1}{3}\ge\frac{1}{m}+\frac{1}{n}+\frac{1}{p}+\frac{1}{q}=\frac{a+b+c+d}{S}=1\)
hay \(\frac{19}{20}\ge1\)(vô lí)
Vậy tồn tại hai cạnh của tứ giác bằng nhau (đpcm)
Gọi S là diện tích tứ giác ABCD có độ dài các cạnh là a,c,c,d. CMR: \(S\le\frac{a^2+b^2+c^2+d^2}{4}\)
theo công thức Brahmagupta bđt \(\Leftrightarrow\)\(\sqrt{\frac{\left(a^2+b^2+c^2+d^2\right)^2-2\left(a^4+b^4+c^4+d^4\right)+8abcd}{16}-\frac{1}{4}\left(ac+bd\right)^2+\frac{1}{4}u^2v^2}\le\frac{a^2+b^2+c^2+d^2}{4}\)
Gọi u, v là 2 đường chéo của tứ giác, theo bđt Ptolemy ta coa: \(uv\le ac+bd\)\(\Leftrightarrow\)\(\frac{1}{4}u^2v^2\le\frac{1}{4}\left(ac+bd\right)^2\)
Do đó cần CM: \(\sqrt{\left(a^2+b^2+c^2+d^2\right)^2-2\left(a^4+b^4+c^4+d^4\right)+8abcd}\le a^2+b^2+c^2+d^2\)
\(\Leftrightarrow\)\(\left(a^2+b^2+c^2+d^2\right)^2-2\left(a^4+b^4+c^4+d^4\right)+8abcd\le\left(a^2+b^2+c^2+d^2\right)^2\)
\(\Leftrightarrow\)\(a^4+b^4+c^4+d^4\ge4abcd\) ( đúng theo Cosi )
Dấu "=" xảy ra khi ABCD là hình vuông
Gọi S là diện tích tứ giác ABCD có độ dài các cạnh là a ; b ; c ; d .
CM \(S\le\frac{a^2+b^2+c^2+d^2}{4}\)
gọi S là diện tích tứ giác ABCD có độ dài các cạnh là a,b,c,d .
Chứng minh rằng : S ≤( a2+b2+c2+d2 )/4