Số nghiệm phức của phương trình  z + 2 | z | + 3 - i = ( 4 + i ) | z | z là

A. 1.

B. 2.

C. 3.

D. 4.

Số phức thỏa mãn phương trình z + 3 z ¯   = ( 2 + i ) 3 ( 2 - i )  Mô đun của số phức w = z + 10 i  là

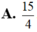
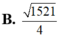
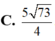
Phương trình: ( z   +   3   -   i ) 2 - 6(z + 3 - i) + 13 = 0 có 2 nghiệm phân biệt. Khẳng định nào sau đây là đúng?

A. Trong 2 nghiệm có một nghiệm bằng 0.

B. Cả 2 nghiệm đều là số thực.

C. Cả 2 nghiệm đều là số thuần ảo.

D. Trong 2 nghiệm có 1 nghiệm là số thực, 1 nghiệm là số thuần ảo.

Cho phương trình z 3   + a z 2   + b z   + c   =   0  Nếu z=1-i và z=1 là 2 nghiệm của phương trình thì a - b - c  bằng

A. 2

B. 3

C. 5

D. 6

Cho phương trình z 3 + a z 2 + b z + c = 0  nhận z = 2  và z = 1 + i  làm các nghiệm của phương trình. Khi đó a - b + c  là