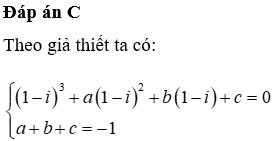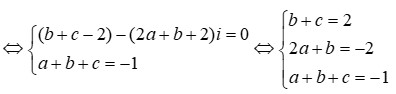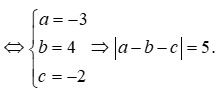Các câu hỏi tương tự
Cho phương trình
z
3
+
a
z
2
+
b
z
+
c
0
. Nếu
z
1
−
i
và
z
1
là hai nghiệm của phương trình thì
a
−
b
−
c
bằng (a, b, c là số thực). A. 2 B. 3 C. 5 D. 6
Đọc tiếp
Cho phương trình z 3 + a z 2 + b z + c = 0 . Nếu z = 1 − i và z = 1 là hai nghiệm của phương trình thì a − b − c bằng (a, b, c là số thực).
A. 2
B. 3
C. 5
D. 6
Nếu z = i là nghiệm phức của phương trình: z 2 + a z + b = 0 với (a,bϵR) thì a+b bằng
A. -1
B. -2
C. 1
D. 2
Nếu z = i là một nghiệm của phương trình z 2 + a z + b = 0 với a , b ∈ ℝ thì a+b bằng
A. 2
B. -1
C. 1
D. -2
Nếu
z
i
là nghiệm phức của phương trình
z
2
+
a
z
+
b
0
với
a
,
b
∈
ℝ
thì
a
+
b
bằng A. -1. B. 2. C. -2. D. 1.
Đọc tiếp
Nếu z = i là nghiệm phức của phương trình z 2 + a z + b = 0 với a , b ∈ ℝ thì a + b bằng
A. -1.
B. 2.
C. -2.
D. 1.
Nếu z = i là một nghiệm của phương trình z 2 + a z + b = 0 với a , b ∈ ℝ thì a + b bằng
A. 2
B. -1
C. 1
D. -2
Nếu z = i là nghiệm phức của phương trình z 2 + a z + b = 0 v ớ i a , b ∈ ℝ thì a + b bằng
A. -1
B. 2
C. -2
D. 1
Nếu z = i là một nghiệm phức của phương trình z 2 + a z + b = 0 với a , b ∈ ℝ thì a + b bằng
A. -2
B. -1
C. 1
D. 2
Cho phương trình
z
2
+
a
z
+
b
0
. Nếu phương trình nhận z 2 + i là một nghiệm thì
a
2
+
b
2
có giá trị bằng A. 36 B. 28 C. 41 D. 48
Đọc tiếp
Cho phương trình z 2 + a z + b = 0 . Nếu phương trình nhận z = 2 + i là một nghiệm thì a 2 + b 2 có giá trị bằng
A. 36
B. 28
C. 41
D. 48
Cho phương trình
z
2
+
a
z
+
b
0
. Nếu phương trình nhận z 2 + i là một nghiệm thì
a
2
+
b
2
có giá trị bằng A. 36 B. 28 C. 41 D. 48
Đọc tiếp
Cho phương trình z 2 + a z + b = 0 . Nếu phương trình nhận z = 2 + i là một nghiệm thì a 2 + b 2 có giá trị bằng
A. 36
B. 28
C. 41
D. 48