Đặt t = 2 - 3 x . Tính 7 + 4 3 x theo t.
![]()
![]()
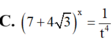
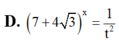
Cho biểu thức Q=/x-3/+/x+2/. Tính tổng T các số nguyên x khi Q đặt GTNN
Tính các tích phân sau: ∫ - 3 2 d x x + 7 + 3 (đặt t = x + 7 hoặc t = x + 7 + 3)
cho bt P =x-2\(\sqrt{2x}\) -3
a) Đặt t=√2x2x -3 hãy tính biểu thức P
b) Tìm GTNN của P
cho bt P =x-2\(\sqrt{2x}\) =3
a) Đặt t=\(\sqrt{2x}\) -3 hãy tính biểu thức P
b) Tìm GTNN của P
1) TÌM X:
a) (2x-1)^2008=(2x-1)^2010
b)4^x -12*2^x+32=0 (đặt t=2^x>9)
2) Cho x^3-x=8 Tính A=x^6-2x^4-x+x^2+x^3
Tính các nguyên hàm sau bằng phương pháp đổi biến số :
a) \(\int x^2\sqrt[3]{1+x^3}dx\) với \(x>-1\) (đặt \(t=1+x^3\))
b) \(\int xe^{-x^2}dx\) (đặt \(t=x^2\))
c) \(\int\dfrac{x}{\left(1+x^2\right)^2}dx\) (đặt \(t=1+x^2\))
d) \(\int\dfrac{1}{\left(1-x\right)\sqrt{x}}dx\) (đặt \(t=\sqrt{x}\))
e) \(\int\sin\dfrac{1}{x}.\dfrac{1}{x^2}dx\) (đặt \(t=\dfrac{1}{x}\))
g) \(\int\dfrac{\left(\ln x\right)^2}{x}dx\) (đặt \(t=\ln x\))
h) \(\int\dfrac{\sin x}{\sqrt[3]{\cos^2x}}dx\) (đặt \(t=\cos x\) )
i) \(\int\cos x\sin^3xdx\) (đặt \(t=\sin x\))
k) \(\int\dfrac{1}{e^x-e^{-x}}dx\) (đặt \(t=e^x\) )
l) \(\int\dfrac{\cos x+\sin x}{\sqrt{\sin x-\cos x}}dx\) (đặt \(t=\sin x-\cos x\))
Tính các tích phân sau: ∫ - 2 4 x - 2 x + 3 2 d x (đặt t = x + 3)
Đặt tính rồi tính:
42 x 2
13 x 3
Tính các tích phân sau bằng phương pháp đổi biến số :
a) \(\int\limits^2_1x\left(1-x\right)^5dx\) (đặt \(t=1-x\))
b) \(\int\limits^{\ln2}_0\sqrt{e^x-1}dx\) (đặt \(t=\sqrt{e^x-1}\))
c) \(\int\limits^9_1x\sqrt[3]{1-x}dx\) (đặt \(t=\sqrt[3]{1-x}\) )
d) \(\int\limits^1_{-1}\dfrac{2x+1}{\sqrt{x^2+x+1}}dx\) (đặt \(u=\sqrt{x^2+x+1}\))
e) \(\int\limits^2_1\dfrac{\sqrt{1+x^2}}{x^4}dx\) (đặt \(t=\dfrac{1}{x}\) )
Tính các tích phân sau :
a) \(\int\limits^4_{-2}\left(\dfrac{x-2}{x+3}\right)^2dx\) (đặt \(t=x+3\) )
b) \(\int\limits^6_{-4}\left|x+3\right|-\left|x-4\right|dx\)
c) \(\int\limits^2_{-3}\dfrac{dx}{\sqrt{x+7}+3}\) (đặt \(t=\sqrt{x+7}\) hoặc \(t=\sqrt{x+7}+3\) )
d) \(\int\limits^{\dfrac{\pi}{2}}_0\dfrac{\cos x}{1+4\sin x}dx\)
e) \(\int\limits^2_1\dfrac{x^9}{x^{10}+4x^5+4}dx\) (đặt \(t=x^5\) )
g) \(\int\limits^3_0\left(x+2\right)e^{2x}dx\)
h) \(\int\limits^5_2\dfrac{\sqrt{4+x}}{x}dx\) (đặt \(t=\sqrt{4+x}\) )