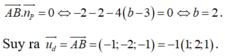Trong không gian Oxyz, mặt phẳng (P): 2x+6y+z-3=0 cắt trục Oz và đường thẳng d: x - 5 1 = y 2 = z - 6 - 1 lần lượt tại A và B. Phương trình mặt cầu đường kính AB là
![]()
![]()
![]()
![]()
Trong không gian Oxyz, mặt phẳng (P):2x+6y+z-3=0 cắt trục Oz và đường thẳng d d : x - 5 1 = y 2 = z - 6 - 1 lần lượt tại A và B. Phương trình mặt cầu đường kính AB là
A. x + 2 2 + y - 1 2 + z + 5 2 = 36
B. x - 2 2 + y + 1 2 + z - 5 2 = 9
C. x + 2 2 + y - 1 2 + z + 5 2 = 9
D. x - 2 2 + y + 1 2 + z - 5 2 = 36
Trong không gian Oxyz, mặt phẳng (P): 2x+6y+z-3=0 cắt trục Oz và đường thẳng d : x - 5 1 = y 2 = z - 6 - 1 lần lượt tại A và B. Phương trình mặt cầu đường kính AB là:
A. x + 2 2 + y - 1 2 + ( z + 5 ) 2 = 36
B. x - 2 2 + y + 1 2 + ( z - 5 ) 2 = 9
C. x + 2 2 + y - 1 2 + ( z + 5 ) 2 = 9
D. x - 2 2 + y + 1 2 + ( z - 5 ) 2 = 36
Đáp án B
Phương pháp:
+) Điểm A thuộc Oz=> A(0;0;0)
+) Điểm B là giao điểm của đường thẳng d và (P) thì tọa độ điểm B thỏa mãn phương trình của d và (P).
+) Phương trình mặt cầu tâm và bán kính R có phương trình là:
![]()
Cách giải:
Phương trình trục Oz
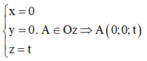
![]()
![]()
![]()
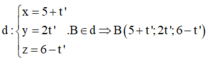
![]()
![]()
![]()
Gọi I là trung điểm của AB => I(2;-1;5)
![]()
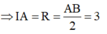
Vậy đường tròn đường kính AB là:
x - 2 2 + y + 1 2 + z - 5 2 = 9
Trong không gian Oxyz, mặt phẳng
P : 2 x + 6 y + z − 3 = 0 cắt trục Oz và đường thẳng d : x − 5 1 = y 2 = z − 6 − 1 lần lượt tại A và B. Phương trình mặt cầu đường kính AB là:
A. x + 2 2 + y − 1 2 + z + 5 2 = 36
B. x − 2 2 + y + 1 2 + z − 5 2 = 9
C. x + 2 2 + y − 1 2 + z + 5 2 = 9
D. x − 2 2 + y + 1 2 + z − 5 2 = 36
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng và mặt cầu (S): x²+y²+z²+2x-6y+4z-15=0. Mặt phẳng chứa d, tiếp xúc với (S) và cắt trục Oz tại điểm có cao độ lớn hơn 3 có phương trình là:
A. 2x-3y+4z-10=0.
B. 2x-3y+4z-12=0.
C. 3x-4y+2z-12=0.
D. 3x-4y+2z-10=0.
Chọn D
Mặt cầu (S) có tâm I (-1;3;-2) và bán kính R = √29.
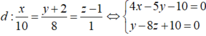
Mặt phẳng (P) chứa d có dạng m (4x-5y-10)+n (y-8z+10)=0
ó 4mx + (n – 5m)y – 8nz + 10n – 10m = 0 với m²+n²>0.
(P) tiếp xúc với (S) nên d (I, (P)) = R
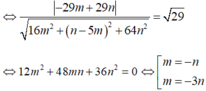
Trường hợp 1: m = -n, phương trình mặt phẳng (P): 2x-3y+4z-10=0.
Khi đó giao điểm của (P) và Ox có tọa độ là (0;0;5/2) (nhận)
Trường hợp 2: m = -3n, phương trình mặt phẳng (P):x-2y+6z-10=0.
Khi đó giao điểm của (P) và Ox có tọa độ là (0;0;5/3) (loại).
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng ∆ : x - 2 1 = y - 2 1 = z - 1 2 và mặt phẳng (α):x+y+z-1=0. Gọi d là đường thẳng nằm trên (α) đồng thời cắt đường thẳng ∆ và trục Oz. Một véctơ chỉ phương của d là:
A. u → = 1 ; - 2 ; 1
B. u → = 1 ; 1 ; - 2
C. u → = 2 ; - 1 ; - 1
D. u → = 1 ; 2 ; - 3
Trong không gian với hệ tọa độ Oxyz, cho điểm A (1; 2; 3) và mặt phẳng (P): 2x + y - 4z + 1 = 0, đường thẳng d đi qua điểm A, song song với mặt phẳng (P), đồng thời cắt trục Oz. Viết phương trình tham số của đường thẳng d.
A . x = 1 + 5 t y = 2 - 6 t z = 3 + t
B . x = t y = 2 t z = 2 + t
C . x = 1 + 3 t y = 2 + 2 t z = 3 + t
D . x = 1 - t y = 2 + 6 t z = 3 + t
Chọn B
Gọi B(0; 0; b) là giao điểm của đường thẳng d và trục Oz.
![]()
Vì đường thẳng d song song với mặt phẳng (P) nên:
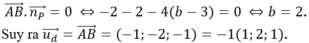
Trong không gian với hệ tọa độ Oxyz, cho điểm A(1;2;3) và mặt phẳng (P): 2x+y-4z+1=0. Đường thẳng (d) qua điểm A, song song với mặt phẳng (P), đồng thời cắt trục Oz. Viết phương trình tham số đường thẳng (d)
A. x = 1 + 5 t y = 2 - 6 t z = 3 + t
B. x = 1 - t y = 2 + 6 t z = 3 + t
C. x = 1 + 3 t y = 2 + 2 t z = 3 + t
D. x = 1 y = 2 t z = 2 + t
Đáp án D
Phương pháp: Giả sử đường thẳng (d) cắt trục Oz tại điểm ![]()
Cách giải:
Giả sử đường thẳng (d) cắt trục Oz tại điểm ![]()
![]()
![]()
![]()
![]()
![]()
Trong không gian với hệ tọa độ Oxyz, cho điểm A(1;2;3) và mặt phẳng (P): 2x+y-4z+1=0. Đường thẳng (d) qua điểm A, song song với mặt phẳng (P), đồng thời cắt trục Oz. Viết phương trình tham số đường thẳng (d)
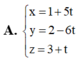
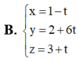
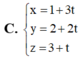
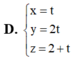
Đáp án D
Phương pháp: Giả sử đường thẳng (d) cắt trục Oz tại điểm B(0;0;b)
![]()
Cách giải:
Giả sử đường thẳng (d) cắt trục Oz tại điểm B(0;0;b)
![]()
![]()
![]()
![]()
Trong không gian với hệ tọa độ Oxyz, cho điểm A (1;2;3) và mặt phẳng (P): 2x+y-4z+1=0, đường thẳng d đi qua điểm A, song song với mặt phẳng (P), đồng thời cắt trục Oz. Viết phương trình tham số của đường thẳng d.
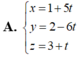
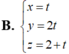
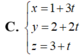
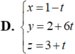
Chọn B
Gọi B (0;0;b) là giao điểm của đường thẳng d và trục Oz.
![]()
Vì đường thẳng d song song với mặt phẳng (P) nên: