Kí hiệu z 0 là nghiệm phức có phần ảo âm của phương trình z 3 − 3 z 2 + 12 z − 10 = 0 . Khi đó điểm nào dưới đây biểu diễn số phức w = i z 0 ?
A. M(3;-1)
B. N(3;1)
C. P(-3;-1)
D. P(-3;1)
Kí hiệu z 1 là nghiệm phức có phần ảo âm của phương trình z 2 − z + 1 = 0 . Trên mặt phẳng tọa độ tìm điểm biểu diễn của số phức w = iz 1 − 3 2 .
A. 1 2 ; 3 2
B. 1 2 ; 0
C. 1 2 ; − 3 2
D. 0 ; 1 2
Kí hiệu z 0 là nghiệm phức có phần ảo âm của phương trình z 2 + z + 1 = 0 . Tìm trên mặt phẳng tọa độ điểm nào dưới đây là điểm biểu diễn số phức w = i z 0 ?
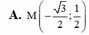
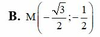
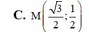
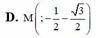
Kí hiệu z 0 là nghiệm phức có phần ảo âm của phương trình z 2 + z + 1 = 0 . Tìm trên mặt phẳng tọa độ điểm nào dưới đây là điểm biểu diễn số phức w=i/ z 0 ?
A. M(- 3 /2;1/2)
B. M(- 3 /2;-1/2)
C. M( 3 /2;1/2)
D. M(-1/2;- 3 /2)
Cho số phức z có phần ảo là số âm và là nghiệm của phương trình z − 2 2 + z 2 = 0 . Môđun của số phức w = i z + 2 z là
A. 2
B. 2 2
C. 2
D. 4
Cho số phức z có phần ảo là số âm và là nghiệm của phương trình z − 2 2 + z 2 = 0. Môđun của số phức w = i z + 2 z là
A. 2
B. 2 2
C. 2
D. 4
Biết z là số phức có phần ảo âm và là nghiệm của phương trình z 2 - 6 z + 10 = 0 Tính tổng phần thực và phần ảo của số phức w = z z ¯
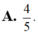
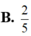
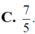
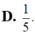
Biết z là số phức có phần ảo âm và là nghiệm của phương trình z 2 − 6 z + 10 = 0. Tính tổng phần thực và phần ảo của số phức w = z z ¯ .
A. 4 5
B. 2 5
C. 7 5
D. 1 5
Nghiệm phức có phần ảo dương của phương trình z2 – z +1 = 0 là z = a + bi, a,b ∈ R. Tính a+ 3 b
A. 2
B. 1
C. –2
D. –1
Đáp án A
Phương pháp :
Tìm nghiệm phức có phần ảo dương của phương trình z2 – z +1 = 0 bằng MTCT.
Cách giải:
Sử dụng MTCT ta tính được nghiệm phức có phần ảo dương của phương trình trên là
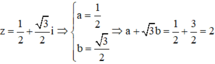
Kí hiệu z 1 là nghiệm phức có phần ảo âm của phương trình z 2 - 2 z + 5 = 0 . Giá trị của z 1 + 2 + 6 i bằng
A. 5
B. 5
C. 73
D. 73
Kí hiệu z 0 là nghiệm phức có phần ảo âm của phương trình 2 z 2 - 6 z + 5 = 0 . Hỏi điểm nào dưới đây là điểm biểu diễn của số phức i z 0 ?
A. M 1 1 2 ; 3 2
B. M 2 3 2 ; 1 2
C. M 3 3 2 ; - 1 2
D. M 4 - 1 2 ; 3 2