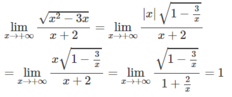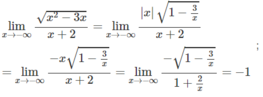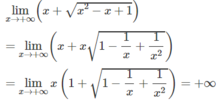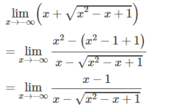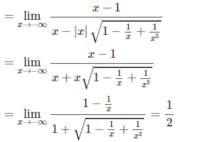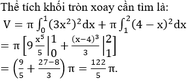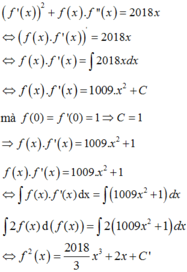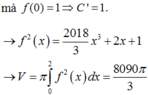Tính giới hạn của các hàm số sau khi x → +∞ và khi x → -∞ f x = x 2 - x - x 2 + 1

Những câu hỏi liên quan
Tính giới hạn của các hàm số sau khi x → +∞ và khi x → -∞ f x = x 2 - 3 x x + 2
Tính giới hạn của các hàm số sau khi x → +∞ và khi x → -∞ f x = x + x 2 - x + 1
Cho hàm số
y
f
(
x
)
3
x
2
khi
x
≤
1...
Đọc tiếp
Cho hàm số y = f ( x ) = 3 x 2 khi x ≤ 1 4 - x khi > 1 . Thể tích của khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi đồ thị hàm số y = f(x) trục hoành và các đường thẳng x = 0, x = 2 quanh trục hoành bằng
A. 29 4
B. 29 π 4
C. 122 15
D. 122 π 15
Tìm a để hàm số sau có giới hạn khi
x
→
2
f
(
x
)
x
2
+
a
x
+
2
khi
x
2...
Đọc tiếp
Tìm a để hàm số sau có giới hạn khi x → 2
f ( x ) = x 2 + a x + 2 khi x > 2 2 x 2 − x + 1 khi x ≤ 2
A. + ∞
B. − ∞
C. 1 2
D.1
Chọn C.
Ta có:
lim x → 2 + f ( x ) = lim x → 2 + ( x 2 + a x + 2 ) = 2 a + 6 .
lim x → 2 − f ( x ) = lim x → 2 − ( 2 x 2 − x + 1 ) = 7 .
Hàm số có giới hạn khi x → 2 ⇔ lim x → 2 + f ( x ) = lim x → 2 − f ( x ) ⇔ 2 a + 6 = 7 ⇔ a = 1 2 .
Vậy a = 1 2 là giá trị cần tìm.
Đúng 0
Bình luận (0)
Cho hai hàm số f(x) và g(x) liên tục trên [a;b] và thỏa mãn
0
g
(
x
)
f
(
x
)
,
∀
x
∈
[
a
;
b
]
.
Gọi V là thể tích của khối tròn xoay sinh ra khi quay quanh Ox hình phẳng (H) giới hạn bởi các đường:
y
...
Đọc tiếp
Cho hai hàm số f(x) và g(x) liên tục trên [a;b] và thỏa mãn 0 < g ( x ) < f ( x ) , ∀ x ∈ [ a ; b ] . Gọi V là thể tích của khối tròn xoay sinh ra khi quay quanh Ox hình phẳng (H) giới hạn bởi các đường: y = f ( x ) , y = g ( x ) , x = a ; x = b . Khi đó V được tính bởi công thức nào sau đây?
A. π ∫ a b f x - g x 2 dx
B. π ∫ a b f 2 x - g 2 x dx
C. π ∫ a b f x - g x dx 2
D. ∫ a b f x - g x dx
Chọn B.
Áp dụng công thức tính thể tích khối tròn xoay: giới hạn bởi đồ thị hàm số y = f(x), y = g(x), x = a, x = b khi quay xung quanh trục Ox
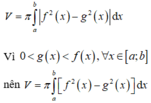
Đúng 0
Bình luận (0)
Cho hai hàm số f(x) và g(x) liên tục trên [a;b] và thỏa mãn
0
g
(
x
)
f
(
x
)
,
∀
x
∈
[
a
;
b
]
.
Gọi V là thể tích của khối tròn xoay sinh ra khi quay quanh Ox hình phẳng (H) giới hạn bởi các đường:
y
f
(
x
)
,
y
...
Đọc tiếp
Cho hai hàm số f(x) và g(x) liên tục trên [a;b] và thỏa mãn 0 < g ( x ) < f ( x ) , ∀ x ∈ [ a ; b ] . Gọi V là thể tích của khối tròn xoay sinh ra khi quay quanh Ox hình phẳng (H) giới hạn bởi các đường: y = f ( x ) , y = g ( x ) , x = a ; x = b . Khi đó V được tính bởi công thức nào sau đây?
A. π ∫ a b f x - g x 2 dx
B. π ∫ a b f 2 x - g 2 x dx
C. π ∫ a b f x - g x dx 2
D. ∫ a b f x - g x dx
Chọn B.
Áp dụng công thức tính thể tích khối tròn xoay: giới hạn bởi đồ thị hàm số y = f(x), y = g(x), x = a, x = b khi quay xung quanh trục Ox
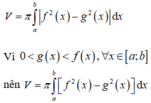
Đúng 0
Bình luận (0)
Câu 1 : Tính thể tích vật thể tròn xoay khi quay hình phẳng (H) giới hạn bởi các đường y = x3 , y = 0, x=0, x=1 quanh trục hoành
Câu 2 : Biết F(x) là một nguyên hàm của hàm f(x) = sin2x và F(π/4) = 1. Tính F(π/6)
1.
\(V=\pi\int\limits^1_0x^6dx=\dfrac{\pi x^7}{7}|^1_0=\dfrac{\pi}{7}\)
2.
\(F\left(x\right)=\int sin2xdx=-\dfrac{1}{2}cos2x+C\)
\(f\left(\dfrac{\pi}{4}\right)=1\Leftrightarrow-\dfrac{1}{2}cos\dfrac{\pi}{2}+C=1\Rightarrow C=1\)
\(\Rightarrow F\left(x\right)=-\dfrac{1}{2}cos2x+1\Rightarrow F\left(\dfrac{\pi}{6}\right)=\dfrac{3}{4}\)
Đúng 2
Bình luận (0)
Cho hàm số f(x) thỏa mãn
f
x
2
+
f
x
.
f
x
2018
x
∀
x
∈
R
và f(0) f’(0) 1. Gọi (H) là hình phẳng giới hạn bởi đồ thị hàm số f(x), trục hoành và hai đường thẳng x 0; x 2. Tính thể tích V của khối tròn xoay tạo thành khi quay (H) quanh trục...
Đọc tiếp
Cho hàm số f(x) thỏa mãn f ' x 2 + f x . f " x = 2018 x ∀ x ∈ R và f(0) = f’(0) = 1. Gọi (H) là hình phẳng giới hạn bởi đồ thị hàm số f(x), trục hoành và hai đường thẳng x = 0; x = 2. Tính thể tích V của khối tròn xoay tạo thành khi quay (H) quanh trục Ox.
A. V = 8090 3 2
B. V = 4036π
C. V = 8090 3 π
D. V = 8090π/3
Gọi `bb A` là giới hạn của hàm số `f(x)=[x+x^2+x^3+...+x^50 -50]/[x-1]` khi `x -> 1.` Tính giá trị của `bb A.`