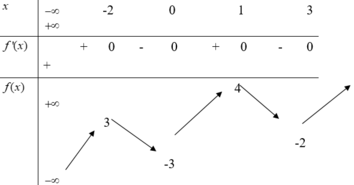
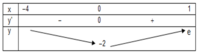
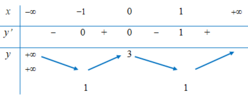
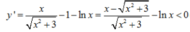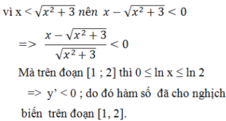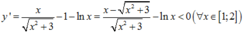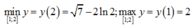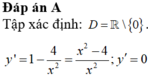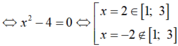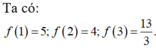Tích giá trị nhỏ nhất và giá trị lớn nhất của hàm số
y
=
x
3
-
3
x
+
3
trên đoạn ![]() bằng
bằng
A. 5.
B. -75.
C. -1.
D. -15.