Trong không gian với hệ trục tọa độ Oxyz, gọi (α) là mặt phẳng cắt ba trục tọa độ tại ba điểm A(2;0;0), B(0;3;0), C(0;0;1) Phương trình của α là
![]()
![]()
![]()
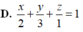
Trong không gian với hệ trục tọa độ Oxyz, gọi α là mặt phẳng cắt ba trục tọa độ tại ba điểm A 2 ; 0 ; 0 , B 0 ; 3 ; 0 , C 0 ; 0 ; 1 . Phương trình của α là
A. x 2 + y 3 + z 1 = 1
B. 3 x + 2 y − 6 z = 0
C. x 2 = y 3 = z 1
D. x 2 + y 3 + z 1 = 0
Đáp án A
Phương trình theo đoạn chắn của mặt phẳng α là x 2 + y 3 + z 1 = 1
Trong không gian với hệ trục tọa độ Oxyz, gọi (α) là mặt phẳng cắt ba trục tọa độ tại ba điểm A 2 ; 0 ; 0 , B 0 ; 3 ; 0 , C 0 ; 0 ; 1 . Phương trình của α là
A. x 2 = y 3 = z 1
B. x 2 + y 3 + z 1 = 0
C. 3 x + 2 y - 6 z = 0
D. x 2 + y 3 + z 1 = 1
Đáp án D
Phương trình theo đoạn chắn của mặt phẳng (α) là x 2 + y 3 + z 1 = 1
Trong không gian Oxyz, phương trình mặt phẳng α cắt ba trục tọa độ tại M - 3 ; 0 ; 0 , N 0 ; 4 ; 0 , P 0 ; 0 ; - 2 có phương trình là:
A. 4 x - 3 y + 6 z + 12 = 0
B. 4 x - 3 y + 6 z - 12 = 0
C. 4 x + 3 y + 6 z + 12 = 0
D. 4 x + 3 y - 6 z + 12 = 0
Trong không gian với hệ tọa độ Oxyz, cho điểm H(1;2;-3). Tìm phương trình mặt phẳng α cắt các trục tọa độ Ox, Oy, Oz lần lượt tại 3 điểm A, B, C sao cho H là trực tâm tam giác ABC.
A. α : x+2y-3z-14=0
B. α : x+2y-3z+4=0
C. α : 6x+3y-2z-18=0
D. α : 6x+3y-2z+8=0
Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng ( α ) : bc . x + ac . y + ab . z - abc = 0 với a, b, c là các số khác 0 thỏa mãn 1 a + 2 b + 3 c = 7 . Gọi A, B, C lần lượt là giao điểm của α với các trục tọa độ Ox, Oy, Oz. Biết mặt phẳng α tiếp xúc với mặt cầu (S): ( x - 1 ) 2 + ( y - 2 ) 2 + ( z - 3 ) 2 = 72 7 . Thể tích khối OABC với O là gốc tọa độ bằng
A. 2 9
B. 3 4
C. 1 8
D. 4 3
Trong không gian với hệ tọa độ Oxyz cho hai điểm A a ; 0 ; - 2 và B 2 ; b ; 0 . Gọi α là mặt phẳng chứa A và trục Oy; β là mặt phẳng chứa B và trục Oz. Biết rằng α và β cắt nhau theo giao tuyến là đường thẳng ∆ có vectơ chỉ phương u → = 2 ; 1 ; 2 . Tính độ dài đoạn thẳng AB
A. A B = 5
B. A B = 2 2
C. A B = 21
D. A B = 2 6

Mặt phẳng
α
chứa A và trục Oy nên có một VTPT là ![]()
Đường thẳng
∆
là giao tuyến của
α
và
β
nên có VTCP ![]()
Theo giả thiết, ta có
u
∆
→
cùng phương với ![]()
Suy ra 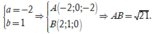
Chọn C.
Trong không gian với hệ tọa độ Oxyz, cho điểm M(1;2;3). Gọi (P) là mặt phẳng đi qua điểm M và cách gốc tọa độ O một khoảng lớn nhất, mặt phẳng (P) cắt các trục tọa độ tại các điểm A, B, C. Tính thể tích khối chóp O.ABC
A. 1372/9
B. 686/9
C. 524/3
D. 343/9
Chọn B
Gọi A(a;0;0), B(0;b;0), C(0;0;c). Ta có phương trình mặt phẳng (P) là: ![]()
Gọi H là hình chiếu của O lên (P). Ta có: d(O, (P)) = OH ≤ OM
Do đó max d(O, (P)) = OM khi và chỉ khi (P) qua M nhận ![]() làm VTPT.
làm VTPT.
Do đó (P) có phương trình:
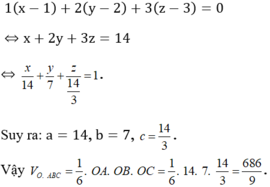
Trong không gian với hệ tọa độ Oxyz, cho điểm M(1;2;3). Gọi (P) là mặt phẳng đi qua điểm Mvà cách gốc tọa độ O một khoảng lớn nhất, mặt phẳng (P) cắt các trục tọa độ tại các điểm A,B,C. Tính thể tích khối chóp O.ABC.
A. 1372 9 .
B. 686 9 .
C. 524 3 .
D. 343 9 .
Trong không gian với hệ tọa độ Oxyz, cho điểm M(1;2;3). Gọi (P) là mặt phẳng đi qua điểm Mvà cách gốc tọa độ O một khoảng lớn nhất, mặt phẳng (P) cắt các trục tọa độ tại các điểm A,B,C. Tính thể tích khối chóp O.ABC.
A. 1372 9
B. 686 9
C. 524 3
D. 343 9