Cho các góc α , β và có số phức z = cos α + i.sin β . Khi đó x = z.w thì:
A . x = cos ( α - β ) + i . sin ( α + β )
B . x = cos ( α + β ) + i . sin ( α + β )
C . x = cos ( α β ) + i . sin ( α β )
D . x = sin ( α - β ) + i . cos ( α + β )
Những câu hỏi liên quan
Cho các góc α, β nhọn và α < β.
CMR : cos(β – α) = cos β. cos α + sin β.sin α .
Cho △ ABC vuông tại A, có AB < AC và trung tuyến AM, góc ACB = α, góc AMB = β. Chứng minh rằng (sin α + cos a)2 = 1 + sin β
Phương trình sin2x=-1/2 có hai họ nghiệm có dạng x=α+kη và x=β+kη, k thuộc z,(-η/4<α<0<β<3η/4).Khi đó tính β2+α2
\(sin2x=-\dfrac{1}{2}\Leftrightarrow\left[{}\begin{matrix}2x=-\dfrac{\pi}{6}+k2\pi\\2x=\dfrac{7\pi}{6}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{\pi}{12}+k\pi\\x=\dfrac{7\pi}{12}+k\pi\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\alpha=-\dfrac{\pi}{12}\\\beta=\dfrac{7\pi}{12}\end{matrix}\right.\) \(\Rightarrow\alpha^2+\beta^2=\dfrac{25\pi^2}{72}\)
Đúng 1
Bình luận (0)
Tìm đẳng thức đúng:A. cos
α
cos
β
B. cos
α
tg
β
C. cos
α
cotg
β
D. cos
α
sin
β
Đọc tiếp
Tìm đẳng thức đúng:
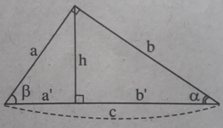
A. cos α = cos β B. cos α = tg β
C. cos α = cotg β D. cos α = sin β
Cho biết 0≤α≤π20≤α≤π2 sao cho
sin3(α)+cos3(α)=1sin3(α)+cos3(α)=1
Và β=sin(α)+cos(α)β=sin(α)+cos(α)
a) Tính ∑α=07π2(sin−1(β)+α)∑α=07π2(sin−1(β)+α)
b) Chứng minh rằng số ββ thỏa đề bài là nghiệm của phương trình: β3−6β+5=0
Trong không gian với hệ trục tọa độ Oxyz, gọi (α) là mặt phẳng chứa đường thẳng
∆
:
x
-
2
1
y
-
1
1
z
-
2
và vuông góc với mặt phẳng (β):x+y+2z+10. Khi đó giao tuyến của hai mặt phẳng (α), (β) có phương trình A. ...
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, gọi (α) là mặt phẳng chứa đường thẳng ∆ : x - 2 1 = y - 1 1 = z - 2 và vuông góc với mặt phẳng (β):x+y+2z+1=0. Khi đó giao tuyến của hai mặt phẳng (α), (β) có phương trình
A. x - 1 = y + 1 1 = z - 1
B. x 1 = y + 1 1 = z - 1 1
C. x - 2 1 = y + 1 - 5 = z 2
D. x + 2 1 = y - 1 - 5 = z 2
Cho các góc α, β nhọn. Chứng minh rằng cos(α + β ) = cosαcosβ - sinαsinβ .
Cho
α
,
β
thỏa mãn
sin
α
+
sin
β
2
2
;
cos
α
+
cos
β
6
2
. Tính
cos
α...
Đọc tiếp
Cho α , β thỏa mãn sin α + sin β = 2 2 ; cos α + cos β = 6 2 . Tính cos α - β .
A. cos α - β = 0
B. cos α - β = 2 2
C. cos α - β = 3 2
D. cos α - β = 1 2
Cho hai số phức α = a + bi, β = c + di. Hãy tìm điều kiện của a, b, c, d để các điểm biểu diễn α và β trên mặt phẳng tọa độ: Đối xứng với nhau qua đường phân giác của góc phần tư thứ nhất và góc phần tư thứ ba