\(a,\left(0,3\right)^{x-3}=1\\ \Leftrightarrow x-3=0\\ \Leftrightarrow x=3\\ b,5^{3x-2}=25\\ \Leftrightarrow3x-2=2\\ \Leftrightarrow3x=4\\ \Leftrightarrow x=\dfrac{4}{3}\\ c,9^{x-2}=243^{x+1}\\ \Leftrightarrow3^{2x-4}=3^{5x+5}\\ \Leftrightarrow2x-4=5x+5\\ \Leftrightarrow3x=-9\\ \Leftrightarrow x=-3\)

d, Điều kiện: \(x>-1;x\ne0\)

\(log_{\dfrac{1}{x}}\left(x+1\right)=-3\\ \Leftrightarrow x+1=x^3\\ x\simeq1,325\left(tm\right)\)

e, Điều kiện: \(x>\dfrac{5}{3}\)

\(log_5\left(3x-5\right)=log_5\left(2x+1\right)\\ \Leftrightarrow3x-5=2x+1\\ \Leftrightarrow x=6\left(tm\right)\)

f, Điều kiện: \(x>\dfrac{1}{2}\)

\(log_{\dfrac{1}{7}}\left(x+9\right)=log_{\dfrac{1}{7}}\left(2x-1\right)\\ \Leftrightarrow x+9=2x-1\\ \Leftrightarrow x=10\left(tm\right)\)

Đáp án A.

Chọn A

Điều kiện: 

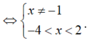
Vậy tập xác định của hàm số f(x) là  suy ra tập xác định của hàm số chứa 4 số nguyên là -3; -2; 0; 1

\(f'\left(x\right)=\dfrac{1}{x\cdot ln10}\)

=>\(f'\left(\dfrac{1}{2}\right)=\dfrac{1}{\dfrac{1}{2}\cdot ln10}=\dfrac{2}{ln10}\)

a)

Điều kiện để $1-2x > 0$ (đối số dương) là:

$1 > 2x$

$x < \frac{1}{2}$

Vậy, để biểu thức $log_3(1-2x)$ có nghĩa, giá trị của $x$ phải nhỏ hơn $\frac{1}{2}$.

b)

Điều kiện để $x+1 \neq 0$ và $x+1 \neq 1$ là:

$x \neq -1$ và $x \neq 0$

Vậy, để biểu thức $log_{x+1}5$ có nghĩa, giá trị của $x$ không được bằng -1 hoặc 0.

\(a,\left(\dfrac{1}{4}\right)^{x-2}=\sqrt{8}\\ \Leftrightarrow\left(\dfrac{1}{2}\right)^{2x-4}=\left(\dfrac{1}{2}\right)^{-\dfrac{3}{2}}\\ \Leftrightarrow2x-4=-\dfrac{3}{2}\\ \Leftrightarrow2x=\dfrac{5}{2}\\ \Leftrightarrow x=\dfrac{5}{4}\)

\(b,9^{2x-1}=81\cdot27^x\\ \Leftrightarrow3^{4x-2}=3^{4+3x}\\ \Leftrightarrow4x-2=4+3x\\ \Leftrightarrow x=6\)

c, ĐK: \(x-2>0\Rightarrow x>2\)

\(2log_5\left(x-2\right)=log_59\\ \Leftrightarrow log_5\left(x-2\right)^2=log_59\\ \Leftrightarrow\left(x-2\right)^2=3^2\\ \Leftrightarrow\left[{}\begin{matrix}x-2=3\\x-2=-3\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=5\left(tm\right)\\x=-1\left(ktm\right)\end{matrix}\right.\)
Vậy phương trình có nghiệm là x = 5.

d, ĐK: \(x-1>0\Leftrightarrow x>1\)

\(log_2\left(3x+1\right)=2-log_2\left(x-1\right)\\ \Leftrightarrow log_2\left(3x+1\right)\left(x-1\right)=2\\ \Leftrightarrow3x^2-2x-1=4\\ \Leftrightarrow3x^2-2x-5=0\\ \Leftrightarrow\left(3x-5\right)\left(x+1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5}{3}\left(tm\right)\\x=-1\left(ktm\right)\end{matrix}\right.\)

Vậy phương trình có nghiệm \(x=\dfrac{5}{3}\)

a) \({\log _{\frac{1}{2}}}\left( {x - 2} \right) =  - 2\)

Điều kiện: \(x - 2 > 0 \Leftrightarrow x > 2\)

Vậy phương trình có nghiệm là \(x = 6\).

b) \({\log _2}\left( {x + 6} \right) = {\log _2}\left( {x + 1} \right) + 1\)

Điều kiện: \(\left\{ \begin{array}{l}x + 6 > 0\\x + 1 > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x >  - 6\\x >  - 1\end{array} \right. \Leftrightarrow x >  - 1\)

Vậy phương trình có nghiệm là \(x = 4\).