Trong không gian cho ba điểm A, B, C.
Tìm tập hợp các điểm M sao cho: M A 2 + 2 M B 2 - 2 M C 2 = k 2 , với k là hằng số
Những câu hỏi liên quan
Trong không gian Oxyz ,cho ba điểm A(1;1;1), B(-1;2;0), C(2;-3;2). Tập hợp tất cả các điểm M cách đều ba điểm A, B, C là một đường thẳng d. Phương trình tham số của d là
Đọc tiếp
Trong không gian Oxyz ,cho ba điểm A(1;1;1), B(-1;2;0), C(2;-3;2). Tập hợp tất cả các điểm M cách đều ba điểm A, B, C là một đường thẳng d. Phương trình tham số của d là
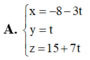
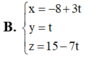
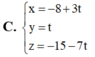
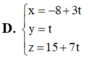
Đáp án A.
(loại B và D).
Xét đáp án A ta có d qua M(-8;0;15)
Đúng 0
Bình luận (0)
Trong không gian cho ba điểm A B C , , cố định không thẳng hàng, tìm tập hợp điểm M sao cho \(\left|\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}\right|=\left|2\overrightarrow{MA}-\overrightarrow{MB}-\overrightarrow{MC}\right|\)
Gọi D là trung điểm BC và G là trọng tâm tam giác ABC
Theo tính chất trọng tâm: \(AG=\dfrac{2}{3}AD\)
\(\left|\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}\right|=\left|2\overrightarrow{MA}-\overrightarrow{MB}-\overrightarrow{MC}\right|\)
\(\Leftrightarrow\left|\overrightarrow{MG}+\overrightarrow{GA}+\overrightarrow{MG}+\overrightarrow{GB}+\overrightarrow{MG}+\overrightarrow{GC}\right|=\left|\overrightarrow{MA}+\overrightarrow{BM}+\overrightarrow{MA}+\overrightarrow{CM}\right|\)
\(\Leftrightarrow\left|3\overrightarrow{MG}+\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}\right|=\left|\overrightarrow{BA}+\overrightarrow{CA}\right|\)
\(\Leftrightarrow\left|3\overrightarrow{MG}\right|=\left|-2\overrightarrow{AD}\right|\)
\(\Leftrightarrow MG=\dfrac{2}{3}AD=AG\)
\(\Rightarrow\) Tập hợp M là mặt cầu tâm G bán kính AG với G là trọng tâm tam giác ABC
Đúng 3
Bình luận (0)
Trong không gian Oxyz, viết phương trình tập hợp các điểm M sao cho
A
M
B
^
90
o
với A ( 2;-1;-3 ); B ( 0;-3;5 ) A.
x
-
1
2
+
y
+
2...
Đọc tiếp
Trong không gian Oxyz, viết phương trình tập hợp các điểm M sao cho A M B ^ = 90 o với A ( 2;-1;-3 ); B ( 0;-3;5 )
A. x - 1 2 + y + 2 2 + z - 1 2 = 18
B. x - 1 2 + y - 2 2 + z - 1 2 = 18
C. x - 1 2 + y + 2 2 + z - 1 2 = 3
D. x - 1 2 + y - 2 2 + z - 1 2 = 3
Tập hợp các điểm M là mặt cầu đường kính AB.
Tâm I là trung điểm AB nên I ( 1;-2;1 )
Bán kính: R = IA = 3 2
Vậy phương trình mặt cầu nói trên là
x - 1 2 + y + 2 2 + z - 1 2 = 18
Đáp án A
Đúng 0
Bình luận (0)
Trong không gian Oxyz, cho ba điểm A(1;1;1), B(-1;2;0), C(2;-3;2). Tập hợp tất cả các điểm M cách đều ba điểm A, B, C là một đường thẳng d. Phương trình tham số của đường thẳng d là:
Đọc tiếp
Trong không gian Oxyz, cho ba điểm A(1;1;1), B(-1;2;0), C(2;-3;2). Tập hợp tất cả các điểm M cách đều ba điểm A, B, C là một đường thẳng d. Phương trình tham số của đường thẳng d là:
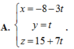
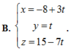
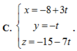
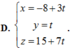
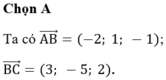
Ta thấy 
không cùng phương nên ba điểm A, B, C không thẳng hàng.
M cách đều hai điểm A, B nên điểm M nằm trên mặt trung trực của AB. M cách đều hai điểm B, C nên điểm M nằm trên mặt trung trực của B, C.
Do đó tập hợp tất cả các điểm m cách đều ba điểm A, B, C là giao tuyến của hai mặt trung trực của AB và BC.
Gọi (P), (Q) lần lượt là các mặt phẳng trung trực của AB và BC. K(0; 3/2; 1/2) là trung điểm AB; N(1/2; -1/2; 1) là trung điểm BC.
(P) đi qua K và nhận 
làm véctơ pháp tuyến nên (P):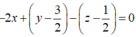 
hay (P): 2x - y + z + 1 = 0
(Q) đi qua N và nhận 
làm véctơ pháp tuyến nên (Q):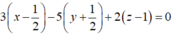 
hay (Q): 3x - 5y +2z - 6 = 0
Ta có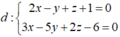 
. Nên d có véctơ chỉ phương 
Cho y = 0 ta sẽ tìm được x = -8, z = 15 nên (-8; 0; 15) ∈ d. Vậy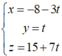 
.
Đúng 0
Bình luận (0)
Trong không gian Oxyz, cho ba điểm A(-6;0;0), B(0;-4;0), C(0;0;6). Tập hợp tất cả các điểm M trong không gian cách đều ba điểm A, B, C là một đường thẳng có phương trình là
Đọc tiếp
Trong không gian Oxyz, cho ba điểm A(-6;0;0), B(0;-4;0), C(0;0;6). Tập hợp tất cả các điểm M trong không gian cách đều ba điểm A, B, C là một đường thẳng có phương trình là
Chọn đáp án C.
Gọi M(x;y;z) ta có
hệ điều kiện
Đúng 0
Bình luận (0)
Cho điểm O cố định, tập hợp tất cả các điểm M trong không gian sao cho
O
M
≤
2
là A. mặt cầu có bán kính bằng 2. B. khối cầu có bán kính bằng 1. C. mặt cầu có bán kính bằng 1 D. khối cầu có bán kính bằng 2.
Đọc tiếp
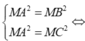
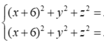
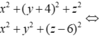
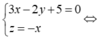
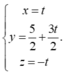
Cho điểm O cố định, tập hợp tất cả các điểm M trong không gian sao cho O M ≤ 2 là
A. mặt cầu có bán kính bằng 2.
B. khối cầu có bán kính bằng 1.
C. mặt cầu có bán kính bằng 1
D. khối cầu có bán kính bằng 2.
Trong không gian với hệ tọa độ Oxyz, cho điểm A(0;0;1), B(-1;-2;0), C(2;0;-1). Tập hợp các điểm M cách đều ba điểm A,B,C là đường thẳng
△
. Viết phương trình đường thẳng
△
.
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho điểm A(0;0;1), B(-1;-2;0), C(2;0;-1). Tập hợp các điểm M cách đều ba điểm A,B,C là đường thẳng △ . Viết phương trình đường thẳng △ .
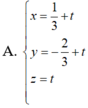
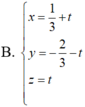
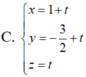
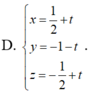
1.Cho tập hợp M={a;b;c}.Viết các tập hợp con của tập hợp M sao cho mỗi tập hợp con đó có 2 phần tử
2..Gọi A là tập hợp các học sinh của lớp 6A có 2 điểm 10 trở lên,B tập hợp các học sinh của lớp 6A có 3 điểm 10 trở lên,M
là tập hợp các học sinh của lớp 6A có 4 điểm 10 trở lên.Dùng kí hiệu tập hợp con để thể hiện quan hệ giữa hai trong ba tập hợp trên
Bt1:
L= { a ; b }
X= { a ; c }
C= { b ; c }
Đúng 0
Bình luận (0)
Trong không gian cho hai điểm A, B cố định. Tập hợp tất cả các điểm M trong không gian thoả mãn
∠
A
M
B
90
°
là A. Mặt cầu đường kính AB B. Mặt cầu đường kính AB nhưng bỏ đi hai điểm A, B C. Khối cầu đường kính AB D. Khối cầu đường kính AB nhưng bỏ đi hai điểm A, B
Đọc tiếp
Trong không gian cho hai điểm A, B cố định. Tập hợp tất cả các điểm M trong không gian thoả mãn ∠ A M B = 90 ° là
A. Mặt cầu đường kính AB
B. Mặt cầu đường kính AB nhưng bỏ đi hai điểm A, B
C. Khối cầu đường kính AB
D. Khối cầu đường kính AB nhưng bỏ đi hai điểm A, B