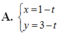
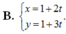
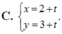
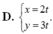
1. trong mặt phẳng tọa độ oxy đường thẳng (d) có pt y = ax + b . Tìm a và b để ( d ) đi qua M ( 1,-2) và N với đường thẳng y = x + 1
Sửa đề: (d)//y=x+1
Để (d) song song với đường thẳng y=x+1 thì \(\left\{{}\begin{matrix}a=1\\b\ne1\end{matrix}\right.\)
hay (d): y=x+b
Vì (d) đi qua M(1;-2) nên Thay x=1 và y=-2 vào hàm số y=x+b, ta được:
\(b+1=-2\)
hay b=-3
Vậy: a=1 và b=-3
Đề thiếu (N ... với đường thẳng y = x + 1)
Trong không gian với hệ trục tọa độ Oxyz, cho đường thẳng ∆ : x - 1 2 = y - 1 1 = z - 1 - 1 và mặt phẳng P : x+y+z-3=0. Gọi d là đường thẳng nằm trong (P), đi qua giao điểm của Δ và (P), đồng thời vuông góc với Δ. Giao điểm của đường thẳng d với mặt phẳng tọa độ (Oxy) là
A. M(2;2;0)
B. M(-3;2;0)
C. M(-1;4;0)
D. M(-3;4;0)
Trong mặt phẳng tọa độ Oxy, cho đường thẳng d: x-2y+1=0. Nếu đường thẳng ∆ qua điểm M (1;-1) và ∆ song song với d thì ∆ có phương trình là
A. x-2y+3=0
B. x-2y-3=0
C. x-2y+5=0
D. x+2y+1=0
Trong mặt phẳng tọa độ Oxy, cho đường thẳng d: x-2y+1=0. Nếu đường thẳng ∆ qua điểm M (1;-1) và ∆ song song với d thì ∆ có phương trình là:
Trong mặt phẳng tọa độ Oxy,cho đường thẳng (d):y=2x+6
a, viết phương trình đường thẳng đi qua M(3;4) và song song với đường thẳng (d)
b, tính khoảng cách từ gốc tọa độ O đến đường thẳng (d)
Trong mặt phẳng tọa độ Oxy, cho đường thẳng d : y = m x + 5.
a) Chứng minh đường thẳng (d) luôn đi qua điểm A(0;5) với mọi giá trị của m.
Thay tọa độ điểm A(0;5) vào phương trình đường thẳng d : y = m x + 5. ta được:
5=m.0+5 luôn đúng với mọi giá trị của tham số m nên đường thẳng (d) luôn
đi qua điểm A với mọi giá trị của m.
a) Trong mặt phẳng tọa độ Oxy cho đường thẳng (d) có phương trình 2x-3y+1=0
Lập pt đường thẳng(d') qua M(-1',1)và song song với(d)
b)Trong mặt phẳng hệ tọa độ Oxy,cho elip có pt(E):x\(\frac{x^2}{49}+\frac{y^2}{25}=1\)
tính chu vi,diện tích hình chữ nhật của elip
Trong mặt phẳng tọa độ Oxy, đường thẳng đi qua điểm M 1 ; 2 và vuông góc với đường thẳng d : 4 x + 2 y + 1 = 0 có phương trình tổng quát là
A. 4 x - 2 y + 3 = 0
B. 2 x - 4 y + 4 = 0
C. 2 x - 4 y - 6 = 0
D. x - 2 y + 3 = 0
Bài 8: Trong mặt phẳng tọa độ Oxy, cho đường thẳng d:\(\left\{{}\begin{matrix}x=-2-2t\\y=1+2t\end{matrix}\right.\left(t\in R\right)\) và điểm A(3;1).
1) Viết phương trình đường thẳng d’ đi qua A và vuông góc với đường thẳng d.
2) Tìm tọa độ giao điểm H của đường thẳng d và d’.
3) Xác định tọa độ điểm A’ đối xứng với A qua đường thẳng d.
4) Tìm tọa độ điểm M nằm trên đường thẳng d sao cho tổng khoảng cách MA+MO là nhỏ nhất.
5) Viết phương trình đường tròn (C) có tâm I nằm trên đường thẳng d và đi qua hai điểm A, O.
1: (d): x=-2-2t và y=1+2t nên (d) có VTCP là (-2;2)=(-1;1) và đi qua B(-2;1)
=>(d') có VTPT là (-1;1)
Phương trình (d') là;
-1(x-3)+1(y-1)=0
=>-x+3+y-1=0
=>-x+y+2=0
2: (d) có VTCP là (-1;1)
=>VTPT là (1;1)
Phương trình (d) là:
1(x+2)+1(y-1)=0
=>x+y+1=0
Tọa độ H là;
x+y+1=0 và -x+y+2=0
=>x=1/2 và y=-3/2
trong mặt phẳng tọa độ oxy cho đthang (d)=(a+1)x+b xác định a;b biết đường thẳng (d) đi qua A(1;5) và có hệ số góc bằng 3
Theo đề, ta có hệ:
a+1=3 và 3*1+b=5
=>b=1 và a=2
