Cho hàm số y=f(x) có đạo hàm y ' = x 2 - 3 x + m 2 + 5 m + 6 . Tìm tất cả các giá trị của m để hàm số đồng biến trên (3;5)
A. ![]()
B.![]()
C. ![]()
D. Với mọi ![]()
Cho hàm số y=f(x) có đạo hàm f'(x)= x ( x - 1 ) 2 ( x 2 + m x + 9 ) . Có bao nhiêu số nguyên dương m để hàm số y=f(3-x) đồng biến trên khoảng ( 3 ; + ∞ ) .
A. 6.
B. 8.
C. 5.
D. 7.
Bài 1: Xét tính đơn điệu của hàm số \(y=f(x)\) khi biết đạo hàm của hàm số là:
a) \(f'(x)=(x+1)(1-x^2)(2x-1)^3\)
b) \(f'(x)=(x+2)(x-3)^2(x-4)^3\)
Bài 2: Cho hàm số \(y=f(x)\) có đạo hàm \(f'(x)=x(x+1)(x-2)\). Xét tính biến thiên của hàm số:
a) \(y=f(2-3x)\)
b) \(y=f(x^2+1)\)
c) \(y=f(3x+1)\)
Câu 5. Cho hàm số f x có đạo hàm liên tục tên R và có đạo hàm ' 2 f x x x 9 1 .Tìm m để hàm số 2 y f x x m 2 đồng biến trên 1,3
Cho hàm số y = f ( x ) có đạo hàm f ' ( x ) = ( x + 1 ) ( x - 2 ) 2 ( x - 3 ) 3 ( x + 5 ) 4 . Hỏi hàm số y = f ( x ) có mấy điểm cực trị?
A. 2
B. 3
C. 4
D. 5
Chọn A
f ' ( x ) đổi dấu khi x chạy qua -1 và 3 nên hàm số có 2 điểm cực trị.
Cho hàm số y=f(x) có đạo hàm trên ℝ . Đồ thị hàm số y=f'(x) như hình vẽ bên dưới
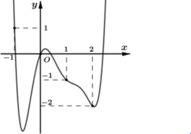
Tìm m để bất phương trình m - x ≥ 2 f x + 2 + 4 x + 3 nghiệm đúng với mọi x ∈ - 3 ; + ∞
A. m ≥ 2 f ( 0 ) - 1
B. m ≤ 2 f ( 0 ) - 1
C. m ≤ 2 f ( - 1 )
D. m ≥ 2 f ( - 1 )
Đáp án B
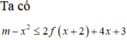
![]()
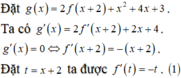
(1) là phương trình hoành độ giao điểm của đồ thị f'(t) và đường thẳng d : y = -t (hình vẽ)
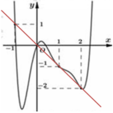
Dựa vào đồ thị của f'(t) và đường thẳng y =-t ta có



Cho hàm số y = f ( x ) có đạo hàm f ' ( x ) = ( x - 2 ) ( x 2 - 3 ) ( x 4 - 9 ) . Số điểm cực trị của hàm số y = f ( x ) là
A. 3
B. 4
C. 2
D. 1
Cho hàm số y = f(x) xác định trên tập số thực R và có đạo hàm f'(x) = (x - sinx)(x- m- 3)(x- \(\sqrt{9-m^2}\) )3 ∀x∈ R (m là tham số). Có bao nhiêu giá trị nguyên của m để hàm số y =f(x) đạt cực tiểu tại x = 0
\(f'\left(x\right)=0\Rightarrow\left[{}\begin{matrix}x-sinx=0\\x-m-3=0\\x-\sqrt{9-m^2}=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=m+3\\x=\sqrt{9-m^2}\end{matrix}\right.\)
Do hệ số bậc cao nhất của x dương nên:
- Nếu \(m=-3\Rightarrow f'\left(x\right)=0\) có nghiệm bội 3 \(x=0\) \(\Rightarrow x=0\) là cực tiểu (thỏa mãn)
- Nếu \(m=3\Rightarrow x=0\) là nghiệm bội chẵn (không phải cực trị, ktm)
- Nếu \(m=0\Rightarrow x=3\) là nghiệm bội chẵn và \(x=0\) là nghiệm bội lẻ, đồng thời \(x=0\) là cực tiểu (thỏa mãn)
- Nếu \(m\ne0;\pm3\) , từ ĐKXĐ của m \(\Rightarrow-3< m< 3\Rightarrow\left\{{}\begin{matrix}m+3>0\\\sqrt{9-m^2}>0\end{matrix}\right.\)
Khi đó \(f'\left(x\right)=0\) có 3 nghiệm pb trong đó \(x=0\) là nghiệm nhỏ nhất
Từ BBT ta thấy \(x=0\) là cực tiểu
Vậy \(-3\le m< 3\)
Cho hàm số y=f(x) liên tục trên R, có đạo hàm f ’ ( x ) = x ( x – 1 ) 2 ( x + 1 ) 3 . Đồ thị hàm số y=f(x) có bao nhiêu điểm cực trị?
A. Đồ thị hàm số f(x) không có điểm cực trị
B. Đồ thị hàm số f(x) có 1 điểm cực trị
C. Đồ thị hàm số f(x) có 2 điểm cực trị
D. Đồ thị hàm số f(x) có 3 điểm cực trị
Cho y = f ( x ) có đạo hàm f ' ( x ) = ( x - 2 ) ( x - 3 ) 2 . Khi đó số cực trị của hàm số y = f ( 2 x + 1 ) là
A. 0
B. 2
C. 1
D. 3
Cho hàm số y=f(x) có đạo hàm f ' ( x ) = x ( x - 2 ) 2 ( 2 x + m + 1 ) ∀ x ∈ ℝ Có bao nhiêu số nguyên âm m để hàm số g ( x ) = f ( x 2 ) đồng biến trên khoảng
A. 5
B. 2
C. 3
D. 4