Cho a > b > 0 . Đường elip (E) có phương trình x 2 a 2 + y 2 b 2 = 1 . Diện tích của hình elip (E) là
A. a 2 + b 2 2 π
B. 2 πab
C. 4 πab
D. πab
Cho a > b > 0 . Đường elip E có phương trình x 2 a 2 + y 2 b 2 = 1 . Diện tích của hình elip E là
A. πab
B. 4 πab
C. a 2 + b 2 2 π
D. 2 πab
Đáp án A
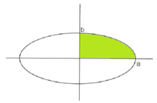
Xét hình phẳng D giới hạn bởi các trục Ox, Oy và đồ thị của hàm số 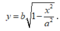
Diện tích elip bằng 4 lần diện tích hình phẳng D.
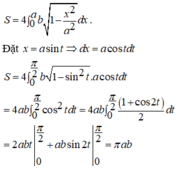
Trong mặt phẳng tọa độ cho hai điểm A(3;0), B(0;2) và đường thẳng d: x + y = 0.
a) Lập phương trình tham số của đường thẳng Δ đi qua A và song song với d
b) Lập phương trình đường tròn đi qua A,B và có tâm thuộc đường thẳng d
c) Lập phương trình chính tắc của elip đi qua điểm B và có tâm sai e = 5 3
Đường thẳng Δ song song với d ⇒ Δ: x + y + c = 0, (c ≠ 0)
Vì Δ đi qua A ⇒ 3 + 0 + c = 0 ⇒ c = -3(tm)
Vậy đường thẳng Δ có dạng: x+y-3=0
Vì đường tròn có tâm I thuộc d nên I(a;-a)
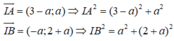
Vì đường tròn đi qua A, B nên I A 2 = I B 2 ⇒ (3 - a ) 2 + a 2 = a 2 + (2 + a ) 2 ⇔ (3 - a ) 2 = (2 + a ) 2
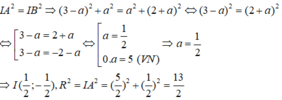
Vậy phương trình đường tròn có dạng:
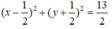
Ta có:
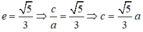
Giả sử elip (E) có dạng:
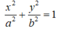
Vì (E) đi qua B nên:
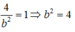
Mà
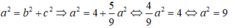
Vậy phương trình chính tắc của elip (E) là:
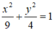
Cho elip (E) có phương trình x²/16 + y²/9 =1. Viết phương trình đường thẳng (d) đi qua M(1;2) và cắt (E) tại A, B sao cho M là trung điểm AB
Cho elip (E) có một đỉnh là A( 5; 0) và có 1 tiêu điểm F1(- 4; 0). Phương trình chính tắc của elip là:
A. x 2 25 + y 2 16 = 1.
B. x 2 5 + y 2 4 = 1.
C. x 2 25 + y 2 9 = 1.
D. x 5 + y 4 = 1.
a) Trong mặt phẳng tọa độ Oxy cho đường thẳng (d) có phương trình 2x-3y+1=0
Lập pt đường thẳng(d') qua M(-1',1)và song song với(d)
b)Trong mặt phẳng hệ tọa độ Oxy,cho elip có pt(E):x\(\frac{x^2}{49}+\frac{y^2}{25}=1\)
tính chu vi,diện tích hình chữ nhật của elip
Cho elip (E) có phương trình: x 2 100 + y 2 36 = 1
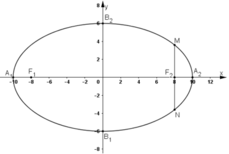
a, Hãy xác định tọa độ các đỉnh, các tiêu điểm của elip (E) và vẽ elip đó.
b, Qua tiêu điểm của elip dựng đường song song với Oy và cắt elip tại hai điểm M và N. Tính độ dài đoạn MN.
a) (E): 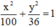 có a = 10; b = 6 ⇒ c2 = a2 – b2 = 64 ⇒ c = 8.
có a = 10; b = 6 ⇒ c2 = a2 – b2 = 64 ⇒ c = 8.
+ Tọa độ các đỉnh của elip là: A1(-10; 0); A2(10; 0); B1(0; -6); B2(0; 6)
+ Tọa độ hai tiêu điểm của elip: F1(-8; 0) và F2(8; 0)
+ Vẽ elip:
b) Ta có: M ∈ (E) ⇒ MF1 + MF2 = 2a = 20 (1)
MN // Oy ⇒ MN ⊥ F1F2 ⇒ MF12 – MF22 = F1F22 = (2c)2 = 162
⇒ (MF1 + MF2).(MF1 – MF2) = 162
⇒ MF1 – MF2 = 12,8 (Vì MF1 + MF2 = 20) (2).
Từ (1) và (2) ta có hệ phương trình
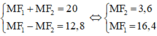
Vậy MN = 2.MF2 = 7,2.
Cho một elip (E) : \(x^2+4y^2=16\)
a) Xác định tọa độ các tiêu điểm và các đỉnh của elip (E)
b) Viết phương trình đường thẳng \(\Delta\) đi qua điểm \(M\left(1;\dfrac{1}{2}\right)\) và có vectơ pháp tuyến \(\overrightarrow{n}=\left(1;2\right)\)
c) Tìm tọa độ các giao điểm A và B của đường thẳng \(\Delta\) và elip (E). Chứng minh MA = MB
Cho elip (E) có các tiêu điểm F 1 - 5 ; 0 , F 2 5 ; 0 và một điểm M nằm trên (E) sao cho chu vi của tam giác M F 1 F 2 bằng 30. Khi đó phương trình chính tắc của elip là:
A. x 2 75 + y 2 100 = 1
B. 100 x 2 + 75 y 2 = 1
C. 75 x 2 + 100 y 2 = 1
D. x 2 100 + y 2 75 = 1
a, cho elip (E) có phương trình chính tắc x^2/49+y^2/25=1. tìm toạ độ các giao điểm của (E) với các trục ox,oy và toạ độ các tiêu điểm của (E)