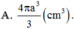
Cho hình chóp S.ABC đáy ABC là tam giác vuông tại C, có cạnh AB a = , cạnh bên SA vuông góc mặt phẳng đáy và SA a = 3 . Tính thể tích V khối cầu ngoại tiếp hình chóp.
A. V= 2 2 3 3 a .
B. V= 3 4a .
C. V= 32 3 3 πa .
D. V= 4 3 3 πa .
Cắt một mặt cầu (S) bởi một mặt phẳng qua tâm được thiết diện là hình tròn có đường kính bằng 4 cm. Tính thể tích của khối cầu.
Trong không gian Oxyz, cho mặt cầu (S) có phương trình là: ( x - 1 ) 2 + ( y - 1 ) 2 + ( z - 3 ) 2 = 4
Cho ba điểm A, M, B nằm trên mặt cầu (S) thỏa mãn điều kiện góc AMB = 90o. Diện tích tam giác AMB có giá trị lớn nhất là:
A. 4
B. 2
C. 4π
D. Không tồn tại
Đáp án A
Ba điểm A, M, B nằm trên mặt cầu (S) thỏa mãn điều kiện = 90°
Nên tam giác AMB vuông tại M.
Ta có: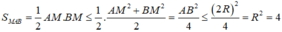 
Dấu bằng xáy ra khi và chỉ khi tam giác MAB vuông cân tại M và AB là một đường kính của mặt cầu (S). Vậy đáp án đúng là A.
Trong không gian với hệ trục toạ độ (Oxyz), cho mặt cầu ( S ) : ( x - 1 ) 2 + ( y - 2 ) 2 + ( z - 3 ) 2 = 9 điểm A(0;0;2). Phương trình mặt phẳng (P) đi qua A và cắt mặt cầu (S) theo thiết diện là hình tròn (C) có diện tích nhỏ nhất là
A. ( P ) : x + 2 y + 3 z + 6 = 0
B. ( P ) : x + 2 y + z - 2 = 0
C. ( P ) : x - 2 y + z - 6 = 0
D. ( P ) : 3 x + 2 y + 2 z - 4 = 0
Trong không gian với hệ trục Oxyz, cho mặt cầu (S) có tâm I (0; -2; 1) và mặt phẳng (P): x + 2y - 2z + 3 = 0. Biết mặt phẳng (P) cắt mặt cầu (S) theo giao tuyến là một đường tròn có diện tích là 2π. Viết phương trình mặt cầu (S).
A. ( S ) : x 2 + ( y + 1 ) 2 + ( z + 1 ) 2 = 3
B. ( S ) : x 2 + ( y + 2 ) 2 + ( z + 1 ) 2 = 1
C . ( S ) : x 2 + ( y + 2 ) 2 + ( z - 1 ) 2 = 3
D. ( S ) : x 2 + ( y + 2 ) 2 + ( z + 1 ) 2 = 2
Chọn C
Ta có h = d(I, (P)) = 1
Gọi (C) là đường tròn giao tuyến có bán kính r.
Vì S = r2.π = 2π <=> r = √2
Mà R2 = r2 + h2 = 3 => R = √3
Vậy phương trình mặt cầu tâm i (0; -2; 1) và bán kính R = √3
Tính diện tích mặt cầu có bán kính R = 2 cm.
\(S=4\pi r^2=4.2^2.\pi=16\pi\left(cm^2\right)\)
Diện tích mặt cầu là:
\(S=4\pi R^2=4.\pi.2^2=16\pi\left(cm^2\right)\)
Diện tích mặt cầu có bán kính R = 2(cm) là:
A. 8π ( c m 2 )
B. 16π ( c m 2 )
C. 32π ( c m 2 )
D. 64π ( c m 2 )
Trong không gian với hệ trục toạ độ (Oxyz), cho mặt cầu (S): (x-1)²+ (y-2)²+ (z-3)²=9, điểm A (0; 0; 2). Phương trình mặt phẳng (P) đi qua A và cắt mặt cầu (S) theo thiết diện là hình tròn (C) có diện tích nhỏ nhất là:
A. (P):x+2y+3z+6=0.
B. (P):x+2y+z-2=0.
C. (P):x-2y+z-6=0.
D. (P):3x+2y+2z-4=0.
Chọn B
Mặt cầu (S): (x-1)²+ (y-2)²+ (z-3)²=9 có tâm I (1;2;3), bán kính R=3.
IA = √6 < R nên A nằm trong mặt cầu.
Gọi r là bán kính đường tròn thiết diện, ta có 
Trong đó h là khoảng cách từ I đến (P).
Diện tích thiết diện là
Vậy diện tích hình tròn (C) đạt nhỏ nhất khi h = IA. Khi đó 
là véc tơ pháp tuyến của (P).
Phương trình mặt phẳng (P) là 1 (x-0)+2 (y-0)+ (z-2)=0 ó x + 2y + z – 2 = 0
Cho mặt cầu (S) có diện tích bằng 4 π . Thể tích khối cầu (S) bằng
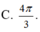
