Trong không gian với hệ trục tọa độ Oxyz, cho ba điểm A (3;2;l), B (l;-1;2), C (l;2;-1). Tìm tọa độ điểm M thỏa mãn O M ⇀ = 2 A B ⇀ - A C ⇀
![]()
![]()
![]()
![]()
Trong không gian với hệ trục tọa độ Oxyz, cho ba điểm A(0; 0; 2), B(3; 0; 5), C(1; 1; 0). Tọa độ của điểm D sao cho ABCD là hình bình hành là
A. D(4; 1; 3)
B. D(-4; -1; -3)
C. D(2; 1; -3)
D. D(-2; 1; -3)
Trong không gian với hệ trục tọa độ Oxyz, cho điểm A(-3;2;-1). Tọa độ điểm A' đối xứng với A qua trục Oy là
A. A'(-3;2;1)
B. A'(3;2;-1)
C. A'(3;2;1)
D. A'(3;-2;-1)
Trong không gian với hệ trục tọa độ Oxyz cho vecto A O → = 3 ( i → + 4 j → ) - 2 k → + 5 j → . Tìm tọa độ điểm A.
A. A(3;5;-2)
B. A(-3;-17;2)
C. A(-3;17;-2)
D. A(3;-2;5)
Trong không gian với hệ trục tọa độ Oxyz cho vecto A O → = 3 ( i → + 4 j → ) - 2 k → + 5 j → . Tìm tọa độ điểm A
A . A ( 3 ; 5 ; - 2 )
B . A ( - 3 ; - 17 ; 2 )
C . A ( - 3 ; 17 ; - 2 )
D . A ( 3 ; - 2 ; 5 )
Trong không gian với hệ trục tọa độ Oxyz, cho ba điểm A (3;2;l), B (l;-1;2), C (l;2;-1). Tìm tọa độ điểm M thỏa mãn O M → = 2 A B → - A C →
A. M (-2;6;-4)
B. M (2;-6;4)
C. M (-2;-6;4)
D. M (5;5;0)
Chọn C.
Phương pháp: Hai véc tơ bằng nhau khi và chỉ khi các tọa độ tương ứng bằng nhau.

Trong không gian với hệ trục tọa độ Oxyz, gọi (α) là mặt phẳng cắt ba trục tọa độ tại ba điểm A(2;0;0), B(0;3;0), C(0;0;1) Phương trình của α là
![]()
![]()
![]()
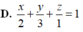
Trong không gian với hệ trục tọa độ Oxyz, cho véc-tơ ![]() . Tìm tọa độ điểm A.
. Tìm tọa độ điểm A.
A. A(-2;3;0)
B. A(-2;0;3)
C. A(0;2;-3)
D. A(0;-2;3).
Trong không gian với hệ trục tọa độ Oxyz, cho ba điểm A 1 ; 1 ; 1 , B 2 ; 3 ; 2 , C 3 ; - 1 ; 3 . Tìm tọa độ điểm D sao cho bốn điểm A, B, C, D lập thành một hình chữ nhật.
A. D(4;1;4)
B. D(2;-3;2)
C. D(4;3;4)
D. D(4;-1;4)
Chọn đáp án A

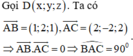
Do đó bốn diểm A, B, C, D lập thành một hình chữ nhật
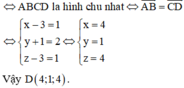

Trong không gian với hệ trục tọa độ Oxyz, cho ba điểm A 2 ; 0 ; 0 ; B 0 ; 3 ; 1 ; C − 1 ; 4 ; 2 . Độ dài đường cao đỉnh A của tam giác ABC
A. 6
B. 2
C. 3 2
D. 3