Gọi S là tập hợp những điểm biểu diễn số phức z thỏa mãn z − 1 − i = 1 . Cho P là một điểm chạy trên S. Khi đó số phức tương ứng với P có môđun lớn nhất bằng?
A. 2 5
B. 1 + 2
C. 2 + 2
D. Không lựa chọn nào đúng
Gọi S là tập hợp những điểm biểu diễn số phức z thỏa mãn z - 1 - i = 1 . Cho P là một điểm chạy trên S. Khi đó số phức tương ứng với P có môđun lớn nhất bằng ?
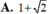
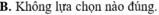
![]()
![]()
Gọi S là tập hợp những điểm biểu diễn số phức z thỏa mãn z - i - 1 = 1 . Cho P là một điểm chạy trên S. Khi đó số phức tương ứng với P có môđun lớn nhất bằng ?
![]()
B. Không lựa chọn nào đúng
![]()
![]()
Gọi S là tập hợp những điểm biểu diễn số phức z thỏa mãn z - 1 - i = 1 . Cho P là một điểm chạy trên S. Khi đó số phức tương ứng với P có môđun lớn nhất bằng ?
A. 1 + 2
B. Không lựa chọn nào đúng.
C. 2 + 2
D. 2 5
Đáp án A
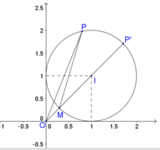
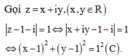
Gọi I là tâm của đường tròn (C).
Với mọi điểm P bất kì chạy trên S, ta có ![]()
do đó số phức tương ứng với P có môđun lớn nhất khi và chỉ khi OP lớn nhất
![]() O, M, P thẳng hàng và M nằm giữa O và P
O, M, P thẳng hàng và M nằm giữa O và P ![]()
Phương trình đường thẳng OI: y = x. Tọa độ P’ là nghiệm của hệ phương trình :

Vậy số phức tương ứng với P có môđun lớn nhất bằng 1 + 2
Gọi M là điểm biểu diễn của số phức z thỏa mãn 3| z + i| = | 2 z ¯ - z + 3i | . Tập hợp tất cả những điểm M như vậy là
A. một parabol.
B. một đường thẳng.
C. một đường tròn.
D. một elip.
Chọn A.
Gọi số phức z = x + yi có điểm biểu diễn là M(x; y) trên mặt phẳng tọa độ:
Theo đề bài ta có:
![]()
⇔ |3(x + yi) + 3i| = |2(x – yi) – (x + yi) + 3i
⇔ |3x + (3y + 3)i| = |x + (3 – 3y)|
![]()
Hay 9x2 + ( 3y + 3) 2 = x2 + ( 3 - 3y) 2
Suy ra: 8x2 + 36y = 0 hay y = -2/9 x2
Vậy tập hợp các điểm M(x; y) biểu diễn số phức z theo yêu cầu của đề bài là parabol 
Tập hợp những điểm M trên mặt phẳng phức biểu diễn số phức z thỏa mãn z + 1 - i + z - 2 + 3 i = 10 có phương trình là
A. x = 2
B. x 2 25 + 4 y 2 75 = 1
C. x 2 25 + 2 y 2 33 = 1
D. Đ á p á n k h á c
Kí hiệu S là tập hợp các điểm biểu diễn số phức z thỏa mãn điều kiện z − 1 + i = z + 2 i và điểm A là điểm biểu diễn số phức 1+2i. Biết rằng M ∈ S là điểm sao cho AM nhỏ nhất. Tung độ của điểm M là giá trị nào sau đây?
A. M − 1 ; 0
B. M 1 ; - 2
C. M − 1 ; 1
D. M 1 ; 1
Cho hai số phức w và z thỏa mãn w - 1 + 2 i = z . Biết tập hợp các điểm biểu diễn của số phức z là đường tròn tâm I(-2;3) bán kính r = 3. Tìm tập hợp các điểm biểu diễn của số phức
A. Là một đường thẳng song song trục tung
B. Là một đường thẳng không song song với trục tung
C. Là đường tròn, tọa độ tâm (-3;5) bán kính bằng 3 5
D. Là đường tròn, tọa độ tâm (-1;1) bán kính bằng 3
Ta có : w - 1 + 2 i = z ⇔ w = z + 1 - 2 i . Suy ra quỹ tích các điểm biểu diễn số phức w có được từ quỹ tích các điểm biểu diễn số phức z bằng cách thực hiện phép tịnh tiến theo v → = ( 1 ; - 2 ) . Do đó quỹ tích quỹ tích các điểm biểu diễn số phức w là đường tròn tâm (-1;1) bán kính bằng 3.
Đáp án D
Xét các số phức z thỏa mãn z - 1 + i ( z + z ¯ ) i + 1 là số thực. Tập hợp các điểm biểu diễn của số phức w = z 2 là parabol có đỉnh
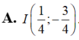
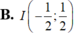
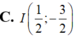
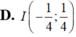
Cho số phức z thỏa mãn: |z - 1 + i| = 2. Tập hợp các điểm trên mặt phẳng tọa độ biểu diễn số phức z là:
A. Một đường thẳng.
B. Một đường Parabol.
C. Một đường tròn có bán kính bằng 2.
D. Một đường tròn có bán kính bằng 4.
Đáp án C
Cách 1: Số phức z được biểu diễn bởi điểm M(x;y).
Số phức z1 được biểu diễn bởi điểm A(1;-1).
Em có: |z - 1 + i| = 2 => MA = 2
Vậy tập hợp điểm M là đường tròn tâm A(1;-1), bán kính R = 2 và có phương trình: ![]()
Cách 2: Đặt ![]() . Số phức z được biểu diễn bởi điểm M(x;y).
. Số phức z được biểu diễn bởi điểm M(x;y).
Em có:
![]()
![]()
![]()
Vậ tập hợp điểm M là đường tròn tâm I(1;-1), bán kính R = 2 và có phương trình: ![]()