Cho ∫ 0 π 4 cos 2 x - 1 d ( cos x ) cos 2 x = a 2 + 2 b a , b ∈ ℤ . Tính S = a 4 - b 4
A. S = 80
B. S = 81
C. S = -80
D. S = -81
Những câu hỏi liên quan
Tính:F=Cos(π/4+α) x cos(π/4-α)
G=Sin(π/3+α) x cos(π/3-α)
H=cos(π/2-α) x sin(π/2+α)
I=sin(π/4+α) - cos(π/4-α)
K=cos(π/6-x) - sin(π/3+x)
Cho 0<α<π va α≠\(\dfrac{\pi}{2}\). Chung minh rang
\(\sqrt{1+cos\alpha}\) + \(\sqrt{1-cos\alpha}\) = 2sin\((\dfrac{\alpha}{2}+\dfrac{\pi}{4}\))
Cho sinα=3/5 và 0<α<π/2. Khi đó, giá trị của A= sin(π−α)+cos(π+α)+cos(−α) là gì?
Online chờ gấp, đa tạ các vị!
`A=sin(π-α)+cos(π+α)+cos(-α)`
`= sinα-cosα+cosα=sinα=3/5`
Đúng 2
Bình luận (0)
Cho 0<α<π/2. Xét dấu A=cos(α+π)
Có bao nhiêu giá trị nguyên của tham số m để phương trình 4cos^3 x - cos 2x + (m-3)cos x - 1 = 0 có đúng 4 nghiệm khác nhau thuộc khoảng (-π/2; π/2)
Xem chi tiết
21 tháng 4 2021 lúc 15:52
Cho \(\sin\alpha=\sqrt{3}\cos\alpha\) và 0 < π < π/2
Tìm \(\sin\alpha,\cos\alpha\)
Chắc là \(0< a< \dfrac{\pi}{2}\)?
\(0< a< \dfrac{\pi}{2}\Rightarrow sina;cosa>0\)
\(\left\{{}\begin{matrix}sina=\sqrt{3}cosa\\sin^2a+cos^2a=1\end{matrix}\right.\) \(\Rightarrow\left(\sqrt{3}cosa\right)^2+cos^2a=1\)
\(\Rightarrow4cos^2a=1\Rightarrow cosa=\dfrac{1}{2}\)
\(\Rightarrow sina=\sqrt{3}cosa=\dfrac{\sqrt{3}}{2}\)
Đúng 2
Bình luận (1)
Cho sin a = 3/5 với π/2 < a < π Tính sin 2a , cos 2a , tan 2a , cot ( a - π/4 ) , sin a/2 , cos a/2 Cảm ơn trc❤
Cho các dòng điện tức thời
i
1
5cos(100
π
t -
π
/3)(A)
i
2
8cos(100
π
t +
π
/6)(A)
i
3
4
2
cos(100
π
t -
π
/4)(A...
Đọc tiếp
Cho các dòng điện tức thời
i 1 = 5cos(100 π t - π /3)(A)
i 2 = 8cos(100 π t + π /6)(A)
i 3 = 4 2 cos(100 π t - π /4)(A)
Xác định những thời điểm tại đó các cường độ dòng điện trên đây đạt :
- Giá trị cực đại hoặc cực tiểu.
- Giá trị cực đại
- Giá trị 0
Cho tan2a = 4/3 với π/2 < a < π. Giá trị cos a là
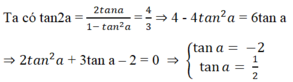
Vì π/2 < a < π nên tan a < 0, do đó tan a = -2.
Áp dụng công thức
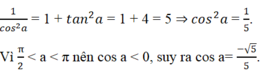
Đáp án là B.
Đúng 0
Bình luận (0)
Dựa vào đồ thị y = cos x trên [-π,π] hãy chỉ ra các khoảng giá trị x mà cos x >0 , cos x < 0