Tìm tập nghiệm s của bất phương trình:
1
3
1
x
3
Đọc tiếp
Tìm tập nghiệm s của bất phương trình: 1 3 1 x > 3
Những câu hỏi liên quan
Tìm tập nghiệm S của bất phương trình
(
3
-
1
)
(
x
+
1
)
)
4
-
2
3
A.
S
[
1
;
+
∞
)
B.
S
(...
Đọc tiếp
Tìm tập nghiệm S của bất phương trình ( 3 - 1 ) ( x + 1 ) ) > 4 - 2 3
A. S = [ 1 ; + ∞ )
B. S = ( 1 ; + ∞ )
C. S = [ - ∞ ; 1 ]
D. S = ( - ∞ ; 1 )
Tìm tập nghiệm S của bất phương trình log0,2 (x – 1) log0,2 (3 – x). A.
S
-
∞
;
3
B.
S
2
;
3
C.
S
2
;...
Đọc tiếp
Tìm tập nghiệm S của bất phương trình log0,2 (x – 1) < log0,2 (3 – x).
A. S = - ∞ ; 3
B. S = 2 ; 3
C. S = 2 ; + ∞
D. S = 1 ; 2
Với m là tham số thực dương khác 1. Hãy tìm tập nghiêm S của bất phương trình
log
m
2
x
2
+
x
+
3
≤
log
m
3
x
2
−
x
.
Biết rằ...
Đọc tiếp
Với m là tham số thực dương khác 1. Hãy tìm tập nghiêm S của bất phương trình log m 2 x 2 + x + 3 ≤ log m 3 x 2 − x . Biết rằng x = 1 là một nghiệm của bất phương trình
A. S = − 2 ; 0 ∪ 1 3 ; 3
B. S = − 1 ; 0 ∪ 1 3 ; 2
C. S = − 1 ; 0 ∪ 1 3 ; 3
D. S = − 1 ; 0 ∪ 1 ; 3
Đáp án C
Vì x = 1 là một nghiệm của bất phương trình
⇒ log m 4 ≤ log m 2 ⇔ log m 2 ≤ 0 ⇔ m ∈ 0 ; 1 .
Khi đó, bất phương trình
log m 2 x 2 + x + 3 ≤ log m 3 x 2 − x ⇔ 3 x 2 − x > 0 2 x 2 + x + 3 ≥ 3 x 2 − x ⇔ − 1 ≤ x < 0 1 3 < x ≤ 3 .
Đúng 0
Bình luận (0)
Với m là tham số thực dương khác 1. Hãy tìm tập nghiêm S của bất phương trình logm(2x2 + x + 3)
≤
logm(3x2 - x). Biết rằng x 1 là một nghiệm của bất phương trình.
Đọc tiếp
Với m là tham số thực dương khác 1. Hãy tìm tập nghiêm S của bất phương trình logm(2x2 + x + 3) ≤ logm(3x2 - x). Biết rằng x = 1 là một nghiệm của bất phương trình.
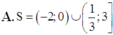
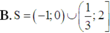
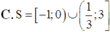
Đáp án C
Vì x = 1 là một nghiệm của bất phương trình
Khi đó, bất phương trình
Đúng 0
Bình luận (0)
Tìm tập nghiệm S của bất phương trình
log
2
2
x
-
3
1
A.
[
2
,
3
)
B.
3
2
,
3
C. [...
Đọc tiếp
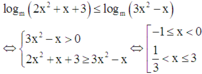
Tìm tập nghiệm S của bất phương trình log 2 2 x - 3 < 1
A. [ 2 , 3 )
B. 3 2 , 3
C. [2,3]
D. - ∞ , 3
1) Tìm tập nghiệm S của bất phương trình | 2x+1| > x+1
2) Tìm tất cả giá trị của tham số m để bất phương trình -x^2+x-m>0 vô nghiệm
2: \(\text{Δ}=1^2-4\cdot\left(-1\right)\cdot\left(-m\right)=1-4m\)
Để bất phương trình vô nghiệm thì \(\left\{{}\begin{matrix}1-4m< 0\\-1< 0\end{matrix}\right.\Leftrightarrow m>\dfrac{1}{4}\)
Đúng 2
Bình luận (0)
Tìm tập nghiệm S của bất phương trình
l
o
g
2
(
1
-
2
x
)
≤
3
.
A.
S
-
7
2
;
-
1
2
B. ...
Đọc tiếp
Tìm tập nghiệm S của bất phương trình l o g 2 ( 1 - 2 x ) ≤ 3 .
A. S = - 7 2 ; - 1 2
B. S = - 7 2 ; + ∞
C. S = - 5 2 ; 1 2
D. S = - 7 2 ; 1 2
Tìm tập nghiệm S của bất phương trình
1
3
x
+
1
-
3
0
Đọc tiếp
Tìm tập nghiệm S của bất phương trình 1 3 x + 1 - 3 > 0
Tìm tập nghiệm S của bất phương trình
log
2
1
-
2
x
≤
3
.
Đọc tiếp
Tìm tập nghiệm S của bất phương trình log 2 1 - 2 x ≤ 3 .
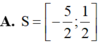
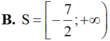
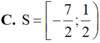
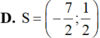
Đáp án C
Điều kiện: x < 1 2 .
Bất phương trình tương đương
1 - 2 x ≤ 8 ⇔ x ≥ - 7 2 ⇒ C h ọ n C .
Đúng 0
Bình luận (0)
Tìm tập nghiệm S của bất phương trình
1
3
x
+
1
-
3
0
A.
S
-
∞
;
-
2
B.
S
-
1
;
+...
Đọc tiếp
Tìm tập nghiệm S của bất phương trình 1 3 x + 1 - 3 > 0
A. S = - ∞ ; - 2
B. S = - 1 ; + ∞
C. S = 1 ; + ∞
D. S = - 2 ; + ∞
Đáp án A
3 - x - 1 > 3 1 → 3 > 1 - x - 1 > 1 ⇔ x < - 2
Đúng 0
Bình luận (0)