Trong không gian với hệ trục Oxyz, cho mặt phẳng (P): 2x+y+2z+2=0 và cho mặt cầu ( x - 2 ) 2 + ( y - 1 ) 2 + ( z - 1 ) 2 = 10 Bán kính của đường tròn giao tuyến giữa (P) và (S) bằng.
![]()
![]()
![]()
![]()
Trong không gian với hệ trục Oxyz, cho mặt phẳng P : 2 x + y + 2 z + 2 = 0 và cho mặt cầu S : x - 2 2 + y - 1 2 + z - 1 2 = 10 Bán kính của đường tròn giao tuyến giữa (P) và (S) bằng.
A. 7
B. 10
C. 3
D. 1
Trong không gian với hệ trục tọa độ Oxyz, cho hai mặt phẳng α : x + y - z + 1 = 0 v à β : - 2 x + m y + 2 z - 2 = 0 . Tìm m để mặt phẳng (α) song song với mặt phẳng (β).
A. m = 2
B. m = 5
C. Không tồn tại
D. m = -2
Trong không gian với hệ trục tọa độ Oxyz, cho mặt cầu ( S ) : x 2 + y 2 + z 2 - 2 x - 2 y - 2 z - 1 = 0 và mặt phẳng ( P ) : x + y + 2 z + 2 = 0 . Giả sử điểm M thuộc (P) và điểm N thuộc (S) sao cho M N → cùng phương với vectơ a → = ( 2 ; - 1 ; 1 ) . Độ dài nhỏ nhất của đoạn MN là:
A. 2 6 +4.
B. 2 6 +2.
C. 2 6 -4.
D. 6 +2.
Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng (P): 2x + y -2z + m = 0 và mặt cầu (S): x2 + y2 + z2 - 2x + 4y -6z - 2= 0. Có bao nhiêu giá trị nguyên của m để mặt phẳng (P) cắt mặt cầu (S) theo giao tuyến là đường tròn (T) có chu vi bằng 4π√3
A. 3
B. 4
C. 2
D. 1
Chọn C
(S) có tâm I (1; -2; 3) và bán kính R = 4
Gọi H là hình chiếu của I lên (P).
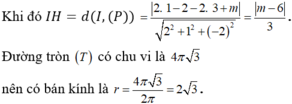
(P) cắt mặt cầu (S) theo giao tuyến là đường tròn (T) có chu vi bằng 4π√3
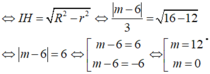
Vậy có 2 giá trị nguyên của m thỏa mãn.
Trong không gian với hệ trục tọa độ Oxyz, cho mặt cầu ( S ) : x 2 + y 2 + z 2 - 2 x - 2 y - 2 z - 1 = 0 và mặt phẳng ( P ) : x + y + 2 z + 2 = 0 . Giả sử điểm M thuộc (P) và điểm N thuộc (S) sao cho M N → cùng phương với vectơ . Độ dài nhỏ nhất của đoạn MN là:
A. 2 6 + 4
B. 2 6 + 2
C. 2 6 - 4
D. 6 + 2
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S): \(x^2+y^2+z^2-2x+6y-8z-10=0\) và mặt phẳng (P): \(x+2y-2z=0\). Viết phương trình mặt phẳng (Q) song song với (P) và tiếp xúc với (S).
Trong không gian với hệ trục tọa độ Oxyz, cho mặt cầu (S) tâm I(1;2;3) và mặt phẳng
(P): 2x - y - 2z + 12 = 0. Biết mặt phẳng (P) cắt mặt cầu (S) theo giao tuyến là đường tròn
có chu vi 6 π . Viết phương trình mặt cầu.
![]()
![]()
![]()
![]()
Trong không gian với hệ trục tọa độ Oxyz, cho mặt cầu (S) tâm I(1;2;3) và mặt phẳng (P): 2x-y-2z+12=0. Biết mặt phẳng (P) cắt mặt cầu (S) theo giao tuyến là đường tròn có chu vi 6 π .Viết phương trình mặt cầu
A. ( x - 1 ) 2 + ( y - 2 ) 2 + ( z - 3 ) 2 = 8
B. ( x - 1 ) 2 + ( y - 2 ) 2 + ( z - 3 ) 2 = 13
C. ( x - 1 ) 2 + ( y - 2 ) 2 + ( z - 3 ) 2 = 9
D. ( x - 1 ) 2 + ( y - 2 ) 2 + ( z - 3 ) 2 = 12
Trong không gian với hệ trục Oxyz , cho hai mặt phẳng α : x + y - z + 1 = 0 và β : - 2 x + m y + 2 z - 2 = 0 . Tìm m để 2 mp song song
A. m=-2
B. m=5
C. Không tồn tại m
D. m=2