Cho hàm số bậc nhất y= ax +b có đồ thị đi qua M(1;4 ) .Đồ thị hàm số y=ax+b cắt trục Ox tại điểm P có hoành độ dương và cắt trục Oy tại Q có tung độ dương . Tìm a,b để OP+OQ nhỏ nhất ( với O là gốc tọa độ)

Những câu hỏi liên quan
Cho hàm số bậc nhất \(y = ax - 4\)
a) Tìm hệ số góc \(a\) biết rằng đồ thị hàm số đi qua điểm \(M\left( {1; - 2} \right)\).
b) Vẽ đồ thị của hàm số.
a) Vì đồ thị hàm số đi qua điểm \(M\left( {1; - 2} \right)\)nên ta có:
\( - 2 = a.1 - 4 \Leftrightarrow a = - 2 + 4 = 2\)
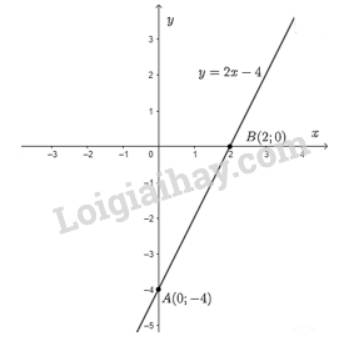
Hàm số cần tìm là \(y = 2x - 4\) có hệ số góc \(a = 2\).
b) Cho \(x = 0 \Rightarrow y = - 4\) ta được điểm \(A\left( {0; - 4} \right)\) trên trục \(Oy\).
Cho \(y = 0 \Rightarrow x = \dfrac{4}{2} = 2\) ta được điểm \(B\left( {2;0} \right)\) trên \(Ox\).
Đồ thị hàm số là đường thẳng đi qua hai điểm \(A\) và \(B\).
Đúng 0
Bình luận (0)
Xác định hàm số bậc nhất y=ax+b biết đồ thị hàm số đi qua A(-1,5) và song song với đồ thị hàm số y=3x+1 biết phương trình của đồ thị hàm số đi qua M(-1,4) và song song với đường thẳng y=2x-1.
Cho hàm số bậc nhất y ax + b. Tìm a và b, biết rằng đồ thị hàm số đi qua điểm M (−1; 1) và cắt trục hoành tại điểm có hoành độ là 5. A.
a
1
6
;
b
5
6
B.
a
−
1
6
;
b
−
5
6
C.
a
1
6...
Đọc tiếp
Cho hàm số bậc nhất y = ax + b. Tìm a và b, biết rằng đồ thị hàm số đi qua điểm M (−1; 1) và cắt trục hoành tại điểm có hoành độ là 5.
A. a = 1 6 ; b = 5 6
B. a = − 1 6 ; b = − 5 6
C. a = 1 6 ; b = − 5 6
D. a = − 1 6 ; b = 5 6
Xác định hàm số bậc nhất y = ax + b. Biết đồ thị hàm số song
song với đường thẳng y = x + 2010 và đi qua điểm M(1 ; –1).
\(\Leftrightarrow\left\{{}\begin{matrix}a=1\\b\ne2010\\a+b=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=1\\b=-2\end{matrix}\right.\Leftrightarrow y=x-2\)
Đúng 1
Bình luận (0)
Cho hàm số bậc nhất y=ax+2
a)Xác định hệ số góc a,biết rằng đồ thị của hàm số đi qua điểm M(1;3)
b)Vẽ đồ thị của hàm số
c)Tính góc tạo bởi đồ thị của hàm số và trục Ox
1) xác định đồ thị hàm số bậc nhất \(y=ax+b\) trong mỗi trường hợp sau:
a) đồ thị hàm số đi qua A(-1; 2), B(2; -3)
b) đồ thị hàm số có hệ số góc là 2 và cắt trục tung tại điểm có tung độ là 2
c) đồ thị hàm số tạo với trục hoành 1 góc \(60^0\) và đi qua điểm B(1; -3)
giúp mk vs ah mk cần gấp
Bài 3. Cho hàm số bậc nhất y = ax – 5 Tìm các giá trị của m để hàm số y = (2m – 4)x + 5
a) Đồng biến trên R. b. Nghịch biến trên R
a) Tìm hệ số góc a, biết đồ thị hàm số y = ax – 5 đi qua điểm A(3 ; 1)
b) Vẽ đồ thị hàm số vừa tìm được ở câu a.
Mn giúp mình với
Bài 3: Xác định hàm số bậc nhất y = ax + b trong mỗi trường hợp sau:
a) Đồ thị của hàm số song song với đường thẳng y = 3x + 1 và đi qua A ( 2; 5)
b) Đồ thị hàm số đi qua A ( -1; 2) và B ( 2; -3).
a: Vì (d) song song với y=3x+1 nên a=1
Vậy: (d): y=x+b
Thay x=2 và y=5 vào (d), ta được:
b+2=5
hay b=3
b: Theo đề,ta có hệ phương trình:
\(\left\{{}\begin{matrix}-a+b=2\\2a+b=-3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-3a=5\\a-b=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-\dfrac{5}{3}\\b=a+2=\dfrac{-5}{3}+2=\dfrac{1}{3}\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Cho hàm số bậc nhất y = ax + 3
a) Xác định hệ số góc a, biết rằng đồ thị của hàm số đi qua điểm A(2; 6).
b) Vẽ đồ thị của hàm số.
Hàm số y = ax + 3 là hàm số bậc nhất nên a ≠ 0
a) Đồ thị của hàm số đi qua điểm A(2; 6) nên:
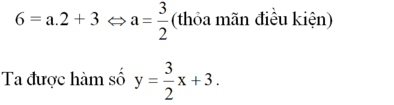
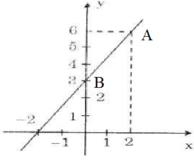
b) Vẽ đồ thị:
- Cho x = 0 thì y = 3 ta được B(0; 3).
Nối A, B ta được đồ thị hàm số
Đúng 0
Bình luận (0)

















