Tích phân I = ∫ 0 1 x - 1 2 x 2 + 1 d x = ln b + c trong đó a,b,c là các số nguyên. Tính giá trị của biểu thức a + b +c
A. 3
B. 0
C. 1
D. 2
Cho hàm số y=f(x) liên tục trên đoạn [0;π/3].Biết f’(x).cosx+f(x).sinx=1, x ϵ [0;π/3] và f(0)=1. Tính tích phân I = ∫ 0 π 3 f x d x
A. 1/2 + π/3
B. 3 + 1 2
C. 3 - 1 2
D. 1/2
Cho hàm số y = f(x) có đạo hàm f’(x) liên tục trên đoạn [0; 1] thỏa mãn f(1) = 1 và I = ∫ 0 1 f x d x = 2 . Tính tích phân I = ∫ 0 1 f ' x d x
A. I = -1.
B. I = 1.
C. I = 2.
D. I = -2.
Chọn D.
Xét I = ∫ 0 1 f ' x d x Đặt t = x → t 2 = x → 2 t d t = d x
Đổi cận x = 0 → t = 0 x = 1 → t = 1 . Khi đó I = 2 ∫ 0 1 t f ' ( t ) d t = 2 A
Tính A = ∫ 0 1 t f ' ( t ) d t . Đặt u = t d v = f ' t d t → d u = d t v = f t
Khi đó
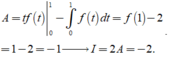
Cho hàm số y = f x = x 2 k h i 0 ≤ x ≤ 2 - x k h i 1 ≤ x ≤
Tính tích phân I = ∫ 0 2 f x d x
A. 5 6
B. 1 3
C. 2
D. 3
Cho hàm số f(x) thỏa mãn ∫ 0 1 ( x + 1 ) f ' ( x ) d x = 10 và 2f(1) - f(0) = 2 .Tính tích phân I = ∫ 0 1 f ( x ) d x .
A. I=-12.
B. I=8.
C. I=12.
D. I=-8
Cho hàm số y = f ( x ) = x 2 k h i 0 ≤ x ≤ 1 2 - x k h i 1 ≤ x ≤ 2
Tính tích phân I= ∫ 0 2 f ( x ) d x
![]()
![]()
![]()
Cho hàm số f x = x + 1 k h i x ≥ 0 e 2 x k h i x ≤ 0 . Tích phân I = ∫ − 1 2 f x d x có giá trị bằng bao nhiêu?
A. I = 7 e 2 + 1 2 e 2 .
B. I = 11 e 2 − 11 2 e 2 .
C. I = 3 e 2 − 1 e 2 .
D. I = 9 e 2 − 1 2 e 2 .
Một học sinh làm bài tích phân I = ∫ 0 1 d x 1 + x 2 theo các bước sau
Bước 1: Đặt x = tan t , suy ra d x = 1 + tan 2 t d t
Bước 2: Đổi x = 1 ⇒ t = π 4 , x = 0 ⇒ t = 0
Bước 3: I = ∫ 0 π 4 1 + tan 2 t 1 + tan 2 t d t = ∫ 0 π 4 d t = t 0 π 4 = 0 − π 4 = − π 4
Các bước làm trên, bước nào bị sai
A. Bước 3
B. Bước 2
C. Không bước nào sai cả
D. Bước 1
Cho hàm số f ( x ) = x + 1 k h i x ≥ 0 e 2 x k h i x ≤ 0 . Tích phân I = ∫ - 1 2 f ( x ) d x có giá trị bằng bao nhiêu?
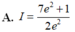
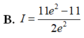
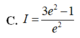
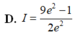
Cho hàm số y = f(x) xác định và liên tục trên 0 ; + ∞ sao cho x 2 + x . f e x + f e x = 1 với mọi x ∈ 0 ; + ∞ Tính tích phân I = ∫ e e ln x . f ( x ) x d x .
A. I = - 1 8 .
B. I = - 2 3 .
C. I = 1 12 .
D. I = 3 8 .
Đáp án C
Phương pháp:
Đặt ẩn phụ t = ln x.
Cách giải:
Ta có:
![]()
![]()
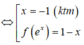
Đặt
![]()
Khi đó :
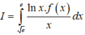
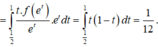
Cho hàm số f(x) có đạo hàm liên tục trên đoạn [0;1] thỏa mãn f(1)=0 và ∫ 0 1 [ f ' ( x ) ] 2 d x = ∫ 0 1 ( x + 1 ) e x f ( x ) d x = e 2 - 1 4 Tính tích phân I= I = ∫ 0 1 f ( x ) d x
A. I=2-e
B. I=e-2
C. I=e/2
D. I = e - 1 2