Trong không gian Oxyz, cho A 4 ; 3 ; - 1 và đường thẳng d : x - 1 2 = y 1 = z - 2 2 .Tìm điểm H thuộc đường thẳng d sao cho AH ngắn nhất.
A. H(3;4;1)
B. H(3;1;4)
C. H - 5 3 ; 1 3 ; - 8 3
D. H 5 3 ; 1 3 ; 8 3
m.n giúp mk 4 bài nì đc ko, mk cần gấp cho ngày mai ak
1/ Trong không gian Oxyz, cho A(3;1), B(2;1), C(2;2). Tìm tọa độ điểm M sao cho \(\overrightarrow{AM}-5\overrightarrow{BM}+3\overrightarrow{CM}=\overrightarrow{0}\)
2/ Trong không gian Oxyz, cho tam giác ABC với A(1;-1), B(2;-4), C(m;2), trọng tâm G của tam giác thuộc trục tung. Khi đó m+8=?
3/ Trong mặt phẳng tọa độ Oxy, hình chiếu của điểm M(13;2) trên trục Oxy là điểm H(a;b). Gía trị của P = 3a + 15b = ?
4/ Trong mặt phẳng tọa độ Oxy, cho tam giác ABC với A(-1;2), B(2;1), C(6;-5) và điểm E thuộc trục Ox thỏa mãn |\(\overrightarrow{EA}+\overrightarrow{EB}+\overrightarrow{EC}\)| min thì tọa độ điểm E là?
mong m.n giúp mk cần rất gấp cho chiều mai, mấy bài này ngoài tầm khả năng lm của mk nên mong m.n cứu mk vs
cho mình hỏi vs
câu 1 trong không gian hệ trục tọa độ Oxyz cho mặt phẳng (A) đi qua hai điểm A( 2;-1;0) và có vecto pháp tuyến n (3:5:4)viết phương trình mặt cầu
câu 2 trong không gian với hệ trục tọa độ Oxyz cho mặt cầu (S) có tâm I(2;-3:7) và đi qua điểm M(-4:0;1) viết phương trình mặt cầu
Trong không gian Oxyz, cho hai điểm A(2;2;2), B(-4;-4;-4). Điểm nào dưới đây nằm trên đường thẳng AB?
A. M 1 (-1; 1; -1)
B. M 2 (1; -1; -1)
C. M 3 (-1; -1; 1)
D. M 4 (-1; -1; -1)
Đáp án D
Ba điểm A, B, M thẳng hàng khi và chỉ khi hai vecto AB ⇀ ; AM → cùng phương
Ta có: ![]()
Do đó, ba điểm A, B, M4 thẳng hàng hay điểm M4 nằm trên đường thẳng AB.
Trong không gian Oxyz, cho điểm A(4;-3;2). Hình chiếu vuông góc của A trên trục Ox là điểm
A. M(4;-3;0)
B. M(4;0;0)
C. M (0;0:2)
D. M (0;-3;0)
Trong không gian Oxyz, cho hai điểm A(2;-1;3), B(3;2;-4). Vectơ A B → có tọa độ là
A. (1;-3;7)
B. (1;3;-7)
C. (-1;3;-7)
D. (-1;-3;-7)
Trong không gian Oxyz, cho ba điểm A(8;0;0), B(0;2;0), C(0;0; - 4). Phương trình mặt phẳng (ABC) là:
A. x + y - 2z = 0
B. x 4 + y 1 + z - 2 = 1
C. x 8 + y 2 + z - 4 = 0
D. x + 4y - 2z - 8 = 0
Đáp án D.
Phương pháp: Viết phương trình mặt phẳng (ABC) dạng đoạn chắn.
Cách giải: Phương trình mặt phẳng (ABC):
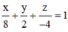
![]()
Trong không gian Oxyz, cho ba điểm A(8;0;0), B(0;2;0), C(0;0;-4). Phương trình mặt phẳng (ABC) là:
A. x+4y-2z=0
B. x 4 + y 1 + z - 2 = 1
C. x 8 + y 2 + z - 4 = 0
D. x+4y-2z-8=0
Đáp án D.
Phương pháp: Viết phương trình mặt phẳng (ABC) dạng đoạn chắn.
Cách giải: Phương trình mặt phẳng (ABC):
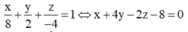
Trong không gian Oxyz, cho hai điểm A(1;3;-1), B(5;4;-4). Khoảng cách giữa hai điểm A và B là:
A. 16
B. 26
C. 2 2
D. 66
Trong không gian Oxyz cho vecto a → = (1; −3; 4). Tìm y 0 và z 0 để cho vecto b → = (2; y 0 ; z 0 ) cùng phương với a →
Ta biết rằng a → và b → cùng phương khi và chỉ khi a → = k b → với k là một số thực. Theo giả thiết ta có: b → = ( x 0 ; y 0 ; z 0 ) với x 0 = 2. Ta suy ra k = 1/2 nghĩa là l = x 0 /2
Do đó: −3 = y 0 /2 nên y 0 = -6
4 = z 0 /2 nên z 0 = 8
Vậy ta có b → = (2; −6; 8)
Trong không gian Oxyz, cho hai điểm A(0;0;3),B(4;−2;7). Mặt cầu đường kính AB có phương trình là
A. x + 2 2 + y - 1 2 + z + 5 2 = 36
B. x - 2 2 + y + 1 2 + z - 5 2 = 9
C. x + 2 2 + y - 1 2 + z + 5 2 = 9
D. x - 2 2 + y + 1 2 + z - 5 2 = 36
Tâm mặt cầu là trung điểm đoạn AB là I(2;-1;5). Bán kính mặt cầu là R = A B 2 = 3
Vậy phương trình mặt cầu x - 2 2 + y + 1 2 + z - 5 2 = 9
Chọn đáp án B.