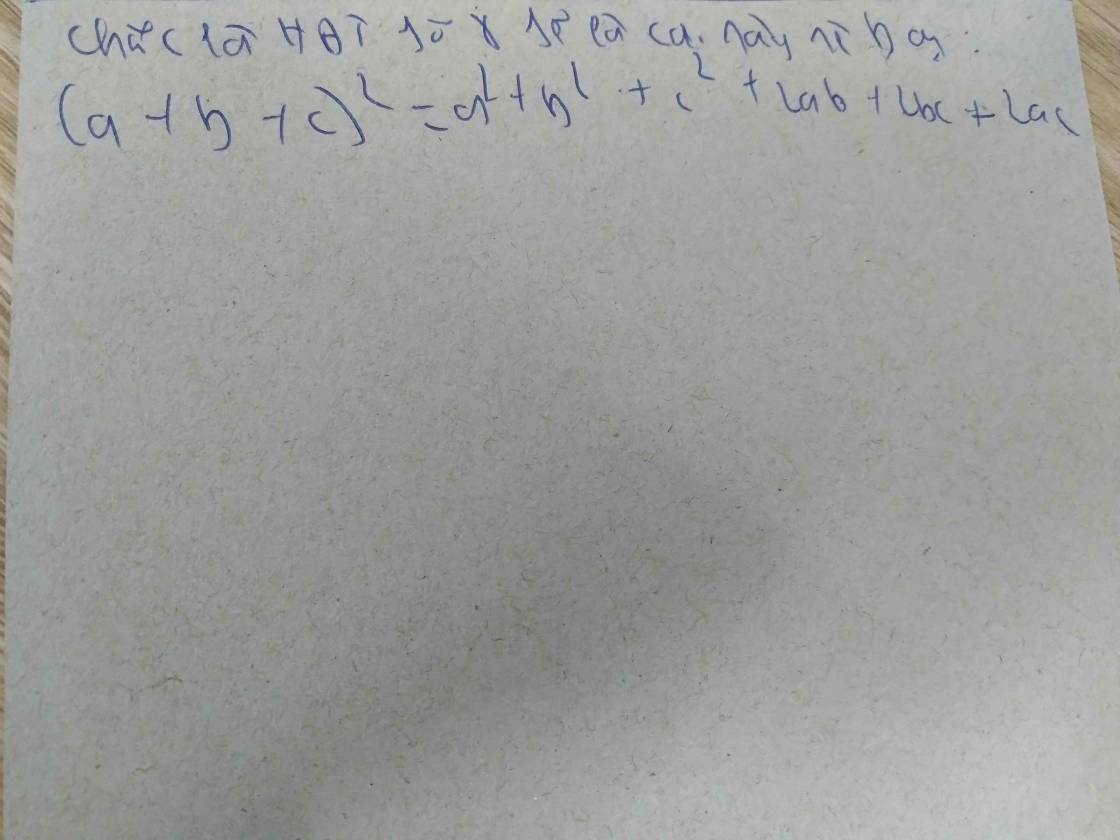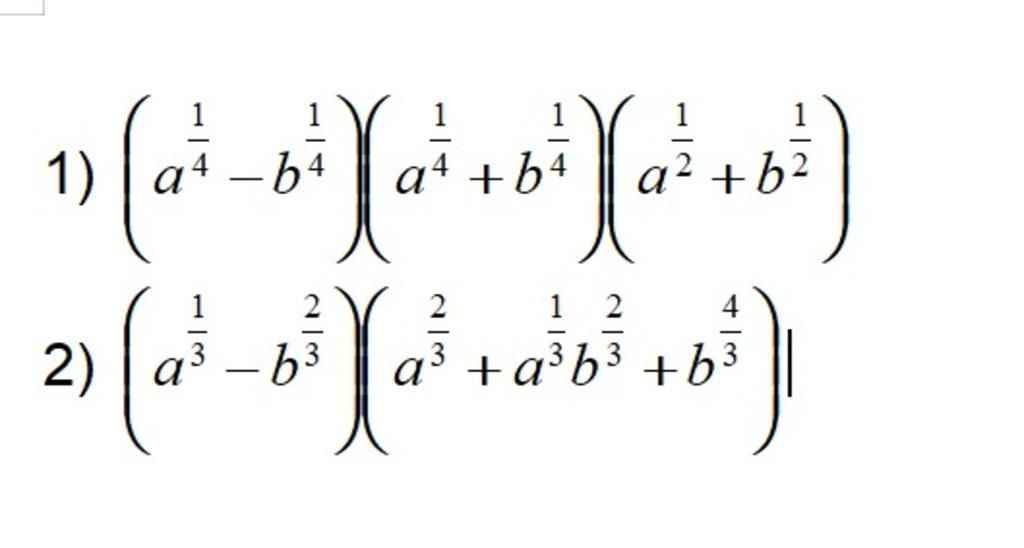
`1)(a^[1/4]-b^[1/4])(a^[1/4]+b^[1/4])(a^[1/2]+b^[1/2])`

`=[(a^[1/4])^2-(b^[1/4])^2](a^[1/2]+b^[1/2])`

`=(a^[1/2]-b^[1/2])(a^[1/2]+b^[1/2])`

`=a-b`

`2)(a^[1/3]-b^[2/3])(a^[2/3]+a^[1/3]b^[2/3]+b^[4/3])`

`=(a^[1/3]-b^[2/3])[(a^[1/3])^2+a^[1/3]b^[2/3]+(b^[2/3])^2]`

`=(a^[1/3])^3-(b^[2/3])^3`

`=a-b^2`

ĐK:  \(x\ge0\)

\(x-6\sqrt{x}+9\)

\(=\left(\sqrt{x}\right)^2-2.\sqrt{x}.3+3^2\)

\(=\left(\sqrt{x}-3\right)^2\)

p/s: do không rõ đề với lại bạn có nhắc tới HĐT nên mk nghĩ đề là như z, sai thì bỏ qua nhé

\(4x^2-4\)  

\(=4\left(x^2-1\right)\) 

\(=4\left(x-1\right)\left(x+1\right)\)

               Bài làm :

Ta có :

\(4x^2-4=\left(2x\right)^2-2^2=\left(2x-2\right)\left(2x+2\right)\)

4x^2-4

= (2x)² - 2²

= (  2x + 2) (2x - 2)

\(25x^2-2=0\)

\(\left(5x\right)^2-\left(\sqrt{2}\right)^2=0\)

Bây giờ mình đã phân tích ra HĐT số 3 rồi nên bạn có thể tự làm!

\(25x^2-2=0\)

\(\Leftrightarrow\left(5x-\sqrt{2}\right)\left(5x+\sqrt{2}\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=\frac{\sqrt{2}}{5}\\x=\frac{-\sqrt{2}}{5}\end{matrix}\right.\)

Kết luận ...

B, C và D

B, C và D không phải hằng đẳng thức

Biểu thức trên ko thể biến đổi ngược thành hằng đẳng thức nhé bạn

Muốn trở thành hằng đẳng thức, có 2 cách

C1: Hằng đẳng thức tổng hai lập phương

\(\left(x+4\right)\left(x^2-4x+16\right)=x^3+64\)

C2: Hằng đẳng thức hiệu hai lập phương

\(\left(x-4\right)\left(x^2+4x+16\right)=x^3-64\)

Ta có :

\(x^3-3x^2-3x+1=0\)

\(\Leftrightarrow x^3+x^2-4x^2-4x+x+1=0\)

\(\Leftrightarrow x^2\left(x+1\right)-4x\left(x+1\right)+\left(x+1\right)=0\)

\(\Leftrightarrow\left(x+1\right)\left(x^2-4x+1\right)=0\)

\(\Leftrightarrow\orbr{\begin{cases}x+1=0\\x^2-4x+1=0\end{cases}}\)\(\Leftrightarrow\orbr{\begin{cases}x=-1\\\left(x-2\right)^2-3=0\end{cases}}\)

\(\Leftrightarrow\orbr{\begin{cases}x=-1\\x=2\pm\sqrt{3}\end{cases}}\)

Vậy tập nghiệm của phương trình là : \(S=\left\{-1;2+\sqrt{3};2-\sqrt{3}\right\}\)