Tích phân ∫ 0 2 d x x + 3 bằng:
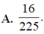
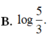
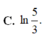
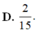
10/ tìm x ( áp dụng kiến thức phân tích đa thức thành nhân tử) a,2-x = 2(x-2)^3 c,(x-1.5)^6 + 2(1,5-x)^3= 0 d,2x^3+3x^2+3+2x =0
a: Ta có: \(2-x=2\left(x-2\right)^3\)
\(\Leftrightarrow2\left(x-2\right)^3+x-2=0\)
\(\Leftrightarrow\left(x-2\right)\left[2\left(x-2\right)^2+1\right]=0\)
\(\Leftrightarrow x-2=0\)
hay x=2
c: Ta có: \(\left(x-1.5\right)^6+2\left(1.5-x\right)^3=0\)
\(\Leftrightarrow\left(x-1.5\right)^6-2\left(x-1.5\right)^3=0\)
\(\Leftrightarrow\left(x-1.5\right)^3\cdot\left[\left(x-1.5\right)^3-2\right]=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1.5\\x=\sqrt[3]{2}+1.5\end{matrix}\right.\)
tìm x biết a, x^4 - 16x^2 = 0 b,x^8 +36x^4 = 0 c,,(x-5)^3-x+5 = 0 d, 5(x-2) -x^2 +4=0 Đây là kiến thức phân tích đa thức thành nhân tử, mn giúp em với
a) Ta có: \(x^4-16x^2=0\)
\(\Leftrightarrow x^2\left(x^2-16\right)=0\)
\(\Leftrightarrow x^2\left(x-4\right)\left(x+4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=4\\x=-4\end{matrix}\right.\)
b) Ta có: \(x^8+36x^4=0\)
\(\Leftrightarrow x^4\left(x^4+36\right)=0\)
\(\Leftrightarrow x^4=0\)
hay x=0
c) Ta có: \(\left(x-5\right)^3-x+5=0\)
\(\Leftrightarrow\left(x-5\right)\cdot\left[\left(x-5\right)^2-1\right]=0\)
\(\Leftrightarrow\left(x-5\right)\left(x-4\right)\left(x-6\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=5\\x=4\\x=6\end{matrix}\right.\)
d) Ta có: \(5\left(x-2\right)-x^2+4=0\)
\(\Leftrightarrow5\left(x-2\right)-\left(x-2\right)\left(x+2\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(5-x-2\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(3-x\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\\x=3\end{matrix}\right.\)
10 Phân tích các đa thức sau thành nhân tử:
a) 5xy(x-y)-2x+2y ; b) 6x-2y-x(y-3x)
c) x^2+4x-xy-4y ; d) 3xy+2z-6y-xz
11 Tìm x, biết: a) 4-9x^2=0 ; b) x^2+x+1/4=0 ; c) 2x(x-3)+(x-3)=0
d) 3x(x-4)-x+4=0 ; e) x^3-1/9x=0 ; f) (3x-y)^2-(x-y)^2=0
a) 5xy ( x - y ) - 2x + 2y
= 5xy ( x - y ) - 2 ( x - y )
= ( x - y ) ( 5xy - 2 )
b) 6x-2y-x(y-3x)
= 2 ( y - 3x ) - x ( y - 3x )
= ( y - 3x ( ( 2 - x )
c) x2 + 4x - xy-4y
= x ( x + 4 ) - y ( x + 4 )
( x + 4 ) ( x - y )
d) 3xy + 2z - 6y - xz
= ( 3xy - 6y ) + ( 2z - xz )
= 3y ( x - 2 ) + z ( x - 2 )
= ( x - 2 ) ( 3y + z )
a,5xy(x-y)-2x+2y=5xy(x-y)-2(x-y)=(x-y)(5xy-2)
b,6x-2y-x(y-3x)=-2(y-3x)-x(y-3x)=(y-3x)(-2-x)
c,x^2+4x-xy-4y=x(x+4)-y(x+4)=(x+4)(x-y)
d,3xy+2z-6y-xz=(3xy-6y)+(2z-xz)=3y(x-2)+z(2-x)=3y(x-2)-z(x-2)=(x-2)(3y-z)
11)
a,4-9x^2=0
(2-3x)(2+3x)=0
2-3x=0=>x=2/3 hoặc 2+3x=0=>x=-2/3
b,x^2 +x+1/4=0
(x+1/2)^2 =0
x+1/2=0
x=-1/2
c,2x(x-3)+(x-3)=0
(x-3)(2x+1)=0
x-3=0=>x=3 hoặc 2x+1=0=>x=-1/2
d,3x(x-4)-x+4=0
3x(x-4)-(x-4)=0
(x-4)(3x-1)=0
x-4=0=>x=4 hoặc 3x-1=0=>x=1/3
e,x^3-1/9x=0
x(x^2-1/9)=0
x(x+1/3)(x-1/3)=0
x=0 hoặc x+1/3=0=>x=-1/3 hoặc x-1/3=0=>x=1/3
f,(3x-y)^2-(x-y)^2 =0
(3x-y-x+y)(3x-y+x-y)=0
2x(4x-2y)=0
4x(2x-y)=0
x=0hoặc 2x-y=0=>x=y/2
1) phân tích thành phân tử:
a) x^3y^3 + 1/125
b) (x+5)^3-(x-5)^3
c) (6-x)^3+(6+x)^3
d) 27x^3 -135x^2+225x-125
2) tìm x:
a)4x^2-25x^4=0
b) x^2-8x+16=0
c)x^3-3x^2+3x-1=0
1.
a) = (xy + \(\frac{1}{5}\)) (x2y2 - \(\frac{xy}{5}\)+ \(\frac{1}{25}\))
b) = (x + 5 - x + 5) [(x+5)2 + (x+5)(x-5) + (x-5)2] = 10 (x2 + 10x + 25 + x2 - 25 + x2 - 10x + 25) = 10 (3x2 +25)
c) = (6 - x + 6 + x) [(6-x)2 - (6-x)(6+x) + (6+x)2] = 12 (36 - 12x + x2 - 26 + x2 + 36 + 12x + x2) = 12 (3x2 + 36) = 12. 3(x2 + 12) = 36(x2 +12)
d) = (3x - 5)3
2.
a) => (2x - 5x2)(2x + 5x2) = 0 ............. giải ra
b) => (x-4)2 = 0 => x - 4 = 0 => x= 4
c) => (x - 1)3 = 0 => x - 1 = 0 => x = 1
. Bài 1: Phân tích đa thức thành nhân tử
a; A = x^3-2x^2-5x+6
b; B = x^4+5x^2+6
c; C = x^4-2x^3+2x-1
d; D = x^3+4x^2+5x+2
. Bài 2: Tìm x
a; x^3-9x^2+14x=0
b; x^3-5x^2+8x-4=0
c; x^4-2x^3+x^2=0
d; 2x^3+x^2-4x-2=0
1.Phân tích đa thức thành nhân tử
a, x^3z+x^2yz-x^2z^2-xyz^2
b, x^3+x^2y-x^2z-xyz
c, a^2x+a^2y+ax+ay+x+y
d, xa+xb+ya+yb-za-zb
2.Phân tích đa thức thành nhân tử
a, a^2+2ab+b^2-c^2+2cd-d^2
b, x^2-4xy+4y^2-x+2y
c,2^2-(x-1)^2+2(x-1)-1
d, xz-yz-x^2+2xy-y^2
3.Tìm x biết
a, x(2x-7)-4x+14 = 0
b, x(x-1)+2x-2 = 0
c, x+x^2-x^2-x^4 = 6
d, 2x^3+3x^2+2x+3 =0
Bài 3:
a: =>(2x-7)(x-2)=0
=>x=7/2 hoặc x=2
b: =>(x-1)(x+2)=0
=>x=1 hoặc x=-2
d: =>2x+3=0
hay x=-3/2
Phân tích thành nhân tử :
a, x - 9 + y - 2√xy (x,y >0)
b, x - 5√x + 6
c, x - 2√x - 3
d, √x - x2
\(a,x-9+y-2\sqrt{xy}\left(x;y>0\right)\)
\(=\left(\sqrt{x}\right)^2-2\sqrt{x}\sqrt{y}+\left(\sqrt{y}\right)^2-9\)
\(=\left(\sqrt{x}-\sqrt{y}\right)^2-9\)
\(=\left(\sqrt{x}-\sqrt{y}+3\right)\left(\sqrt{x}-\sqrt{y}-3\right)\)
\(b,\text{ đkxđ }x\ge0\)
\(x-5\sqrt{x}+6=\left(\sqrt{x}\right)^2-2\sqrt{x}-3\sqrt{x}+6\)
\(=\sqrt{x}.\left(\sqrt{x}-2\right)-3.\left(\sqrt{x}-2\right)=\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)\)
\(c,đ\text{kxđ }x\ge0\)
\(x-2\sqrt{x}-3=\left(\sqrt{x}\right)^2+\sqrt{x}-3\sqrt{x}-3\)
\(=\sqrt{x}\left(\sqrt{x}+1\right)+3.\left(\sqrt{x}+1\right)=\left(\sqrt{x}+1\right)\left(\sqrt{x}+3\right)\)
\(d,\text{đkxđ }x\ge0\)
\(\sqrt{x}-x^2=\sqrt{x}-\left(\sqrt{x}\right)^4=\sqrt{x}\left(1-\left(\sqrt{x}\right)^3\right)\)
\(=\sqrt{x}.\left(1-\sqrt{x}\right)\left(1+\sqrt{x}+x\right)\)
1/phân tích thành phân tử
a. x^6 - 64
b. x^3+3x^2 + 3x+1- y^3
c. x^3 - 27+ x( x-3)
d, y^6 - 625
2/tìm x biết
a. 25x^2 -1=0
b. 4 (x-1)^2 -9 =0
c. 1/4 -9(x-1)^2 =0
d. 1/16 - ( 2x + 3/4) ^2 =0
1/4 nghĩa là 1 phần 4 á nhé, nhờ giúp đỡ
2/
a/ \(25x^2-1=0\)
<=> \(\left(5x\right)^2-1=0\)
<=> \(\left(5x-1\right)\left(5x+1\right)=0\)
<=> \(\orbr{\begin{cases}5x-1=0\\5x+1=0\end{cases}}\)<=> \(\orbr{\begin{cases}x=\frac{1}{5}\\x=-\frac{1}{5}\end{cases}}\)
b/ \(4\left(x-1\right)^2-9=0\)
<=> \(\left[2\left(x-1\right)\right]^2-3^2=0\)
<=> \(\left(2x-2\right)^2-3^2=0\)
<=> \(\left(2x-2-3\right)\left(2x-2+3\right)=0\)
<=> \(\left(2x-5\right)\left(2x+1\right)=0\)
<=> \(\orbr{\begin{cases}2x-5=0\\2x+1=0\end{cases}}\)<=> \(\orbr{\begin{cases}x=\frac{5}{2}\\x=-\frac{1}{2}\end{cases}}\)
c/ \(\frac{1}{4}-9\left(x+1\right)^2=0\)
<=> \(\left(\frac{1}{2}\right)^2-\left[3\left(x-1\right)\right]^2=0\)
<=> \(\left(\frac{1}{2}\right)^2-\left(3x-3\right)^2=0\)
<=> \(\left(\frac{1}{2}-3x+3\right)\left(\frac{1}{2}+3x-3\right)=0\)
<=> \(\left(\frac{7}{2}-3x\right)\left(-\frac{5}{2}+3x\right)=0\)
<=> \(\orbr{\begin{cases}\frac{7}{2}-3x=0\\-\frac{5}{2}+3x=0\end{cases}}\)<=> \(\orbr{\begin{cases}3x=\frac{7}{2}\\3x=\frac{5}{2}\end{cases}}\)
<=> \(\orbr{\begin{cases}x=\frac{7}{6}\\x=\frac{5}{6}\end{cases}}\)
d/ \(\frac{1}{16}-\left(2x+\frac{3}{4}\right)^2=0\)
<=> \(\left(\frac{1}{4}\right)^2-\left(2x+\frac{3}{4}\right)^2=0\)
<=> \(\left(\frac{1}{4}-2x-\frac{3}{4}\right)\left(\frac{1}{4}+2x+\frac{3}{4}\right)=0\)
<=> \(\left(-\frac{1}{2}-2x\right)\left(1+2x\right)=0\)
<=> \(2\left(-\frac{1}{4}-x\right)\left(1+2x\right)=0\)
<=> \(\orbr{\begin{cases}-\frac{1}{4}-x=0\\1+2x=0\end{cases}}\)<=> \(\orbr{\begin{cases}x=-\frac{1}{4}\\x=-\frac{1}{2}\end{cases}}\)
bài 1: Tìm x
a)5(x-1)=x-1
b)x(x-2)+(x-2)=0
c)5x(x-3)-x+3=0
d)x(2x-7)-4x+17=0
bai2:phân tích thành nhân tử
a)2x^2+2y-x^2z+z-y^2z-2
a) 5(x-1)=x-1
5x-5=x-1
5x-x=5-1
4x=4=>x=1
b)x(x-2)+(x-2)=0
(x-2)(x+1)=0
=>x=2 hay x=-1
c)5x(x-3)-x+3=0
5x(x-3)-(x-3)=0
(5x-1)(x-3)=0
=>x=\(\frac{1}{5}\)hay x=3
d)x(2x-7)-4x+17=0
x(2x-7-4)+17=0
x(2x-11)+17=0
=> đa thức này không có nghiệm
Phân tích thành nhân tử
(x-3)^2-5(x-2)+5=0
(2x-1)^2-3(x-2)(x+2)-25=0
\(\left(x-3\right)^2-5\left(x-2\right)+5=0\\ \Leftrightarrow x^2-6x+9-5x+10+5=0\\ \Leftrightarrow x^2-11x+24=0\\ \Leftrightarrow\left(x-8\right)\left(x-3\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=8\\x=3\end{matrix}\right.\)
\(\left(2x-1\right)^2-3\left(x-2\right)\left(x+2\right)-25=0\\ \Leftrightarrow4x^2-4x+1-3\left(x^2-4\right)-25=0\\ \Leftrightarrow4x^2-4x-24-3x^2+12=0\\ \Leftrightarrow x^2-4x-12=0\\ \Leftrightarrow\left(x-6\right)\left(x+2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=6\\x=-2\end{matrix}\right.\)
a: Ta có: \(\left(x-3\right)^2-5\left(x-2\right)+5=0\)
\(\Leftrightarrow x^2-6x+9-5x+10+5=0\)
\(\Leftrightarrow x^2-11x+24=0\)
\(\Leftrightarrow\left(x-8\right)\left(x-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=8\\x=3\end{matrix}\right.\)
b: Ta có: \(\left(2x-1\right)^2-3\left(x-2\right)\left(x+2\right)-25=0\)
\(\Leftrightarrow4x^2-4x+1-3x^2+12-25=0\)
\(\Leftrightarrow x^2-4x-12=0\)
\(\Leftrightarrow\left(x-6\right)\left(x+2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=6\\x=-2\end{matrix}\right.\)